4 ニュートン法(Newton's method)
4.1 計算方法
4.1.1 漸化式
関数
実際にこの数列を計算するためには,漸化式が必要である.図のようにすると,関数![]() 上の点
上の点
![]() の接線を引き,それとx軸と交点が
の接線を引き,それとx軸と交点が![]() になる.まずは,
になる.まずは,
![]() を求めることにする.点
を求めることにする.点
![]() を通り,傾きが
を通り,傾きが
![]() の
直線の方程式は,
の
直線の方程式は,
| (12) |
である.図4より,
となる.これで,
計算の終了は,
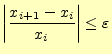 |
(14) |
の条件を満たした場合とするのが一般的である 5.
これは少し高度な内容なので,8節におまけで載せておく.た ぶん,諸君の中の何人かは一瞬にして実数の近似解を求めるニュートン法を理解したと思 う.これまでの話が理解できた者は,8節を勉強することを勧 める.
4.1.2 解への収束速度
ニュートン法を使う上で必要な式は,式(13)のみである.計算 に必要な式は分かったが,数列がどのように真の解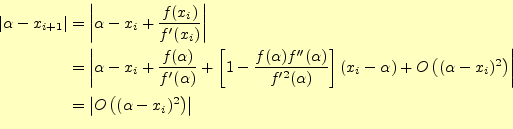 |
となる.
4.1.3 解けない方程式
アルゴリズムから,二分法は解に必ず収束する6.ただし,収束のスピードが遅いのが欠点である. 一方,ニュートン法と解に収束するとは限らない.初期値が悪いと解に収束しない場合が ある.厳密にその条件を求めるのは大変なので,実例を示すことにする.非線形方程式
| (16) |
を計算することを考える.これは,初期値が悪いと収束しない方程式の例である.例えば 初期値
このようにニュートン法は解に収束しないで,振動する場合がある.こうなると,プログ ラムは無限ループに入り,永遠に計算し続ける.これは資源の無駄遣いなので,慎むべき である.通常は,反復回数の上限を決めて,それを防ぐ.ニュートン法を使う場合は,こ の反復回数の上限は必須である.
ニュートン法で収束する必要条件が分かればこの問題は解決する.しかし,それを探すの
は大変である.というか私には分からない.一方,十分条件は簡単にわかる.閉区間
![]() で,
で,
![]() のような関数を考える.このとき,
のような関数を考える.このとき,
- 常に
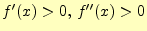 で,初期値が
で,初期値が の場合
の場合
- 常に
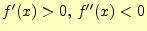 で,初期値が
で,初期値が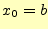 の場合
の場合
実際には収束しない場合のほうが稀であるので,ニュートン法は非常に強力な非線形方程 式の解法である.ただ,反復回数を忘れないことが重要である.また,二分法と組み合わ せて使うことも考えられる.
4.2 フローチャート
二分法同様,関数と計算を打ち切る条件はプログラム中に書くものとする.そうすると, 図7のようなニュートン法のフローチャートが考えられる.ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年7月11日
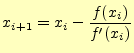
![\includegraphics[keepaspectratio, scale=0.7]{figure/function_solution/NewtonMethod.eps}](img64.png)
![\includegraphics[keepaspectratio, scale=0.4]{figure/comv_hasan/hasan.eps}](img81.png)
![\includegraphics[keepaspectratio, scale=0.4]{figure/comv_hasan/comb.eps}](img82.png)
![\includegraphics[keepaspectratio, scale=0.8]{figure/flow_chart/flow_newton.eps}](img83.png)