勾配から電磁場を求めるのは、静電場の問題に現れる。即ち、
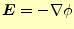 |
(18) |
である。ここではこの勾配の計算方法について述べる。
静電場の問題はスカラーポテンシャルを計算するのが一般的である。それがもっとも計算
が簡単であるからである。我々は、
軸対称構造の静電場
の問題を計算している。軸対
称なので、ポテンシャル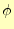 は
は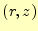 の関数で、
の関数で、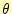 方向には依存しない。従って、こ
のポテンシャルの勾配から求められる電場は、
方向には依存しない。従って、こ
のポテンシャルの勾配から求められる電場は、
となる。
本図書の回転で示したのと同様に、有限要素法では図1で示され
る三角形要素の頂点でスカラーポテンシャル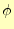 の値を計算する。これら3つのスカラー
ポテンシャルから、要素内の電場
の値を計算する。これら3つのスカラー
ポテンシャルから、要素内の電場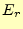 と
と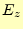 を求めなくてはならない。要素内の任意の位置で
のスカラーポテンシャルをを計算する式を導く。今のところ、我々の計算は1次近似なので、
要素内のスカラーポテンシャルは
を求めなくてはならない。要素内の任意の位置で
のスカラーポテンシャルをを計算する式を導く。今のところ、我々の計算は1次近似なので、
要素内のスカラーポテンシャルは
となる。
ポテンシャルの値が分かれば、電場は計算できる。式(21)を式
(19)や(20)に代入すると、
となる。スカラーポテンシャルの値を示す1次近似の係数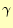 や
や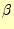 を計算すれば、
電場が分かるのである。非常に単純な式である。
を計算すれば、
電場が分かるのである。非常に単純な式である。
電場を計算するための係数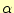 や
や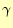 、
、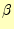 の計算は、回転の場合と同様に
すればよく、
の計算は、回転の場合と同様に
すればよく、
となる。もちろん、
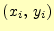 と
と
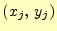 、
、
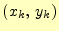 は頂点の座標、
は頂点の座標、
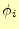 と
と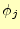 、
、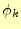 はその位置のスカラーポテンシャルである。これで、要素
内の電場の値は計算できる。
内部要素で共有された頂点での電場の値を求めるときには、回転の時と同様に問題が生じ
る。図2のように要素A,B,C,D,E,Fが、頂点
はその位置のスカラーポテンシャルである。これで、要素
内の電場の値は計算できる。
内部要素で共有された頂点での電場の値を求めるときには、回転の時と同様に問題が生じ
る。図2のように要素A,B,C,D,E,Fが、頂点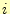 を共有し、
その点での電場の値をどうするかである。A〜Fのそれぞれの要素で電場の値が微妙に異な
ることが問題である。その差は小さいので、とりあえず平均値とするのが良いであろう。
式(22)や(23)を見ても分かるように、
回転の時のように値が発散するようなことはない。しかし、境界条件について、少し考え
てみるのも良かろう。軸対称問題の静電場の場合、その軸上では、自然境界条件
を共有し、
その点での電場の値をどうするかである。A〜Fのそれぞれの要素で電場の値が微妙に異な
ることが問題である。その差は小さいので、とりあえず平均値とするのが良いであろう。
式(22)や(23)を見ても分かるように、
回転の時のように値が発散するようなことはない。しかし、境界条件について、少し考え
てみるのも良かろう。軸対称問題の静電場の場合、その軸上では、自然境界条件
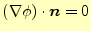 |
(25) |
を満たす必要がある。ここで、
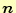 は軸に垂直で外側に向かっている単位ベクトルで
ある。これは、
は軸に垂直で外側に向かっている単位ベクトルで
ある。これは、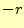 方向を向いている。
方向を向いている。
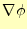 の
の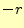 方向成分は、
方向成分は、
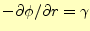 である。従って
である。従って
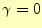 |
(26) |
となる必要がある。
軸上の要素、例えば図3の要素A, B, Cの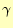 がそのようになってい
るかは不明である。計算精度にも依存するであろう。従って、ここでは変な小細工をしな
いで、軸上でも
がそのようになってい
るかは不明である。計算精度にも依存するであろう。従って、ここでは変な小細工をしな
いで、軸上でも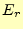 が出てきても、それは計算誤差として考えるのが良いであろう。こ
のことから、我々は回転の計算同様に、図3の要素A, B, Cが共有するノー
ドでの電場(
が出てきても、それは計算誤差として考えるのが良いであろう。こ
のことから、我々は回転の計算同様に、図3の要素A, B, Cが共有するノー
ドでの電場(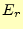 と
と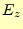 )は、要素AとCの平均とする。要素Bのように軸上の1つのノード
しかない要素は、平均の計算に入れないこととする。
)は、要素AとCの平均とする。要素Bのように軸上の1つのノード
しかない要素は、平均の計算に入れないこととする。
この場合も回転と同様に考える。即ち、図4の様な境界があるとき、
要素A,B,Cが共有するノードの電場の値は、要素AとBの平均とする。要素Bは考えないもの
とする。
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年8月20日
![]() の値を計算する。これら3つのスカラー
ポテンシャルから、要素内の電場
の値を計算する。これら3つのスカラー
ポテンシャルから、要素内の電場![]() と
と![]() を求めなくてはならない。要素内の任意の位置で
のスカラーポテンシャルをを計算する式を導く。今のところ、我々の計算は1次近似なので、
要素内のスカラーポテンシャルは
を求めなくてはならない。要素内の任意の位置で
のスカラーポテンシャルをを計算する式を導く。今のところ、我々の計算は1次近似なので、
要素内のスカラーポテンシャルは
![]() や
や![]() 、
、![]() の計算は、回転の場合と同様に
すればよく、
の計算は、回転の場合と同様に
すればよく、
![]() がそのようになってい
るかは不明である。計算精度にも依存するであろう。従って、ここでは変な小細工をしな
いで、軸上でも
がそのようになってい
るかは不明である。計算精度にも依存するであろう。従って、ここでは変な小細工をしな
いで、軸上でも![]() が出てきても、それは計算誤差として考えるのが良いであろう。こ
のことから、我々は回転の計算同様に、図3の要素A, B, Cが共有するノー
ドでの電場(
が出てきても、それは計算誤差として考えるのが良いであろう。こ
のことから、我々は回転の計算同様に、図3の要素A, B, Cが共有するノー
ドでの電場(![]() と
と![]() )は、要素AとCの平均とする。要素Bのように軸上の1つのノード
しかない要素は、平均の計算に入れないこととする。
)は、要素AとCの平均とする。要素Bのように軸上の1つのノード
しかない要素は、平均の計算に入れないこととする。