回転から電磁場を求めるのは、静磁場と共振空洞の問題に現れる。即ち、
| |
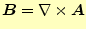 (静磁場) (静磁場) |
(1) |
| |
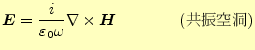 |
(2) |
である。微分(回転)と言う意味では、全く同じ形をしている。そのため、ここでは静磁場
の問題のみについて述べる。共振空洞の場合は同じように考えて欲しい。
軸対称構造、実際には軸対称電磁石
であるが、その場合の有限要素解析では、ベクトルポテンシャルを計算するのが一般的で
ある。軸対称なので、ベクトルポテンシャルは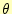 方向成分のみである。従って、こ
のベクトルポテンシャルの回転から求められる磁場は、
方向成分のみである。従って、こ
のベクトルポテンシャルの回転から求められる磁場は、
となる。
有限要素法では、図1に示すように、三角形要素の頂点でベクト
ルポテンシャル
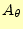 の値を計算する。これら3つのベクトルポテンシャルから、
要素内の磁場
の値を計算する。これら3つのベクトルポテンシャルから、
要素内の磁場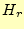 と
と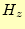 を求めなくてはならない。まず初めに、要素内の任意の位置で
のベクトルポテンシャルを計算する式を導く。今のところ、我々の計算は1次近似なので、
要素内のベクトルポテンシャルは
を求めなくてはならない。まず初めに、要素内の任意の位置で
のベクトルポテンシャルを計算する式を導く。今のところ、我々の計算は1次近似なので、
要素内のベクトルポテンシャルは
となる。
この要素内のベクトルポテンシャルの値を用いて、領域内の磁場を計算することにする。
これは簡単で、式(5)を用いて、式(3)と
(4)を評価すれば良い。これらから
を導くことができる。ここで、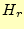 の式に座標
の式に座標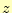 が含まれるのが奇異に感じるかもしれ
ない。これは、要素内でベクトルポテンシャル
が含まれるのが奇異に感じるかもしれ
ない。これは、要素内でベクトルポテンシャル
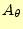 が一定でも、回転が生じるこ
とを考えると理解できる。
が一定でも、回転が生じるこ
とを考えると理解できる。
残りの問題は、ベクトルポテンシャルを1次近似した係数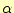 と
と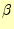 、
、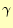 を
求めることである。これが分かれば、要素内の任意の位置での磁場が計算できる。三角形
要素の頂点の座標とベクトルポテンシャルの有限要素法の計算結果によりが分かっている
ので、これら3つの係数を決定することは可能である。これら3点では
を
求めることである。これが分かれば、要素内の任意の位置での磁場が計算できる。三角形
要素の頂点の座標とベクトルポテンシャルの有限要素法の計算結果によりが分かっている
ので、これら3つの係数を決定することは可能である。これら3点では
の関係がある。ここで、
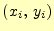 と
と
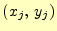 、
、
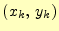 は頂点の座標、
は頂点の座標、
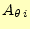 と
と
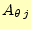 、
、
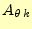 はその位置のベクトルポテンシャ
ルである。この連立方程式から、1次近似の係数は
はその位置のベクトルポテンシャ
ルである。この連立方程式から、1次近似の係数は
と計算できる。これで、要素内の磁場の値は計算できる。
要素内の磁場は、式(6)や(7)を用いて計算
できる。しかし、エレメントの境界での値を考えると問題が生じる。例えば、図
2に示すように要素A,B,C,D,E,Fが共有する頂点の磁場の値
をどうするかである。今のところ、このような場合は平均とするのが良いであろう。
式(7)を見ると、軸上(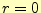 )では問題が起きそうである。ゼロで
割るため発散する可能性がある。問題となるのは、図3に示す要素
うち、AやCのように要素の一辺が軸となる場合とBのように1つの頂点が軸上にある場合で
ある。
)では問題が起きそうである。ゼロで
割るため発散する可能性がある。問題となるのは、図3に示す要素
うち、AやCのように要素の一辺が軸となる場合とBのように1つの頂点が軸上にある場合で
ある。
まずは、要素の一辺が軸となる場合について考える。この要素の軸上のベクトルポテンシャ
ルの値は、物理的にゼロ(
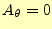 )にならなくてはならない。そのため、要素内の
ベクトルポテンシャルを示す式(5)は、
)にならなくてはならない。そのため、要素内の
ベクトルポテンシャルを示す式(5)は、
| 0 |
 |
(10) |
となる。図3の要素Aの場合、軸となる要素の一辺(
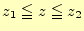 )で、これが成立しなくてはならないので、
)で、これが成立しなくてはならないので、
となる必要がある。要するに、要素の一辺が軸上にある場合、その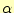 と
と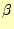 は
ゼロになり、ベクトルポテンシャルは
は
ゼロになり、ベクトルポテンシャルは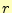 座標に比例しているのである。そのため、式
(7)が発散する事はなく、問題は生じないのである。まとめると、
この場合の軸上の磁場は、
座標に比例しているのである。そのため、式
(7)が発散する事はなく、問題は生じないのである。まとめると、
この場合の軸上の磁場は、
となる。軸上では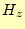 のみで、これは物理的に正しい。非常にめでたい。
のみで、これは物理的に正しい。非常にめでたい。
次に、図3の要素Bのように、頂点の一つが軸上にある場合を考える。こ
の軸上の頂点でのベクトルポテンシャルはゼロなので、
| 0 |
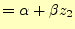 |
(15) |
である。この式は頂点での一点
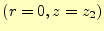 でしか成り立たない。そのため、一辺が軸
上にあるときのような式(11)や(12)に対応するもの
は無い。従って、この要素の軸上の頂点での磁場は
でしか成り立たない。そのため、一辺が軸
上にあるときのような式(11)や(12)に対応するもの
は無い。従って、この要素の軸上の頂点での磁場は
となる。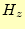 が発散しないのは良いが、
が発散しないのは良いが、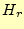 がゼロにならないのはまずい。
がゼロにならないのはまずい。
以上のことから、図3のように軸上のノードの磁場は、図中の要素AやB
のように一辺が軸上にある磁場の平均とするのが良いだろう。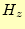 の発散の問題も生じ
ないし、
の発散の問題も生じ
ないし、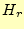 が有限になることもない。
が有限になることもない。
軸上の磁場の計算で示したように、頂点の一つが軸上にある場合、物理的な条件に合致し
ない場合がある。先の場合は、軸上にある一つの頂点での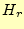 がゼロとならないのであ
る。一方、一辺が軸上にある場合は、物理的な条件に完全に合致している。そのような理
由から、軸上にあるノードでの磁場の値は、それを共有するものうち、軸上に辺がある要
素の平均を取ることにした。
がゼロとならないのであ
る。一方、一辺が軸上にある場合は、物理的な条件に完全に合致している。そのような理
由から、軸上にあるノードでの磁場の値は、それを共有するものうち、軸上に辺がある要
素の平均を取ることにした。
これと同じことが、軸以外の境界でも生じる。特に、境界が直線の場合は、全く同じ状況
になるであろう。このことから、ここでも軸と同じように考えるのが良いだろう。即ち、図
4の様な境界があるとき、要素A,B,Cが共有するノードの磁場の値は、
要素AとBの平均とする。要素Bは考えないものとする。
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年8月20日
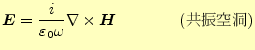
![]() の値を計算する。これら3つのベクトルポテンシャルから、
要素内の磁場
の値を計算する。これら3つのベクトルポテンシャルから、
要素内の磁場![]() と
と![]() を求めなくてはならない。まず初めに、要素内の任意の位置で
のベクトルポテンシャルを計算する式を導く。今のところ、我々の計算は1次近似なので、
要素内のベクトルポテンシャルは
を求めなくてはならない。まず初めに、要素内の任意の位置で
のベクトルポテンシャルを計算する式を導く。今のところ、我々の計算は1次近似なので、
要素内のベクトルポテンシャルは
![]() と
と![]() 、
、![]() を
求めることである。これが分かれば、要素内の任意の位置での磁場が計算できる。三角形
要素の頂点の座標とベクトルポテンシャルの有限要素法の計算結果によりが分かっている
ので、これら3つの係数を決定することは可能である。これら3点では
を
求めることである。これが分かれば、要素内の任意の位置での磁場が計算できる。三角形
要素の頂点の座標とベクトルポテンシャルの有限要素法の計算結果によりが分かっている
ので、これら3つの係数を決定することは可能である。これら3点では
![]() )にならなくてはならない。そのため、要素内の
ベクトルポテンシャルを示す式(5)は、
)にならなくてはならない。そのため、要素内の
ベクトルポテンシャルを示す式(5)は、
![]() の発散の問題も生じ
ないし、
の発散の問題も生じ
ないし、![]() が有限になることもない。
が有限になることもない。