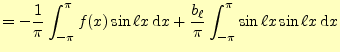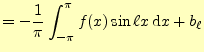4 最良近似としてのフーリエ級数
フーリエ級数とは全く話を別にして,区間と近似する.ここで,式(25)の係数
が最も小さくなるようにする.この二乗平均誤差は,係数
二乗平均誤差を最小にするためには,それぞれの偏微分がゼロになるときに得られる.すなわち,
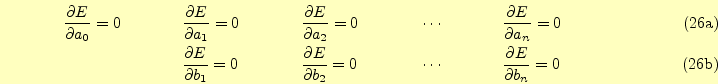 |
が条件となる.この具体的な計算は,式(26)に式(25)を代入 して偏微分がゼロとなる
4.0.0.1 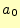 の計算
の計算
二乗平均後差が最小になる| 0 | 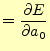 |
|
![$\displaystyle =-\frac{1}{2\pi}\int_{-\pi}^{\pi}2\left\{ f(x)-\left[\frac{a_0}{2}+\sum_{k=1}^n(a_k\cos kx+b_k\sin kx)\right] \right\}\frac{1}{2}\,\mathrm{d}x$](img209.png) |
||
|
式(5)より
| ||
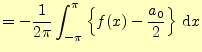 |
||
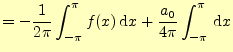 |
||
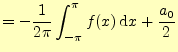 |
(28) | |
である.ゆえに,
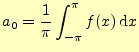 |
(29) |
となる.これは,フーリエ級数の
4.0.0.2 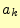 の計算
の計算
二乗平均後差が最小になるしたがって,
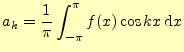 |
(31) |
である.これもフーリエ係数の計算と同じ
4.0.0.3 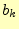 の計算
の計算
同様にし,二乗平均後差が最小になるしたがって,
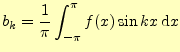 |
(33) |
である.これもフーリエ係数の計算と同じ.
フーリエ級数は,関数![]() を最小二乗法で近似している.これは,展開する三角関数が
有限個の場合でも,その展開の項数に関わらずいつも最良近似となっている.展開の項数
に関わらず,同じ係数でいつでも最良近似となるのは,展開する三角関数の集合が直交関数
系となっているからである.
を最小二乗法で近似している.これは,展開する三角関数が
有限個の場合でも,その展開の項数に関わらずいつも最良近似となっている.展開の項数
に関わらず,同じ係数でいつでも最良近似となるのは,展開する三角関数の集合が直交関数
系となっているからである.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年12月1日
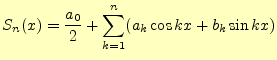
![$\displaystyle E(a_0,\,a_1,\,a_2,\,\cdots,\,a_n;\,b_1,\,b_2,\,\cdots,\,b_n)= \frac{1}{2\pi}\int_{-\pi}^{\pi}[f(x)-S_n(x)]^2\,\mathrm{d}x$](img200.png)
![$\displaystyle =-\frac{1}{2\pi}\int_{-\pi}^{\pi}2\left\{ f(x)-\left[\frac{a_0}{2}+\sum_{k=1}^n(a_k\cos kx+b_k\sin kx)\right] \right\}\cos \ell x\,\mathrm{d}x$](img221.png)
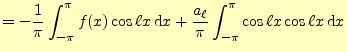
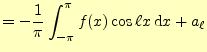
![$\displaystyle =-\frac{1}{2\pi}\int_{-\pi}^{\pi}2\left\{ f(x)-\left[\frac{a_0}{2}+\sum_{k=1}^n(a_k\cos kx+b_k\sin kx)\right] \right\}\sin\ell x\,\mathrm{d}x$](img229.png)