2 周期関数のフーリエ級数
2.1 周期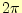 の場合
の場合
2.1.1 三角関数の直交性
関数の集まりのとき,
フーリエ級数は,関数の集まり2
![]() で周期関数を表したものである.これらの関数が直
交関数系になることを示す.フーリエ係数を計算する場合,この直交関係が重要になる.
それを証明するために,次の順序で式(1)の積分を行う.
-4pt
で周期関数を表したものである.これらの関数が直
交関数系になることを示す.フーリエ係数を計算する場合,この直交関係が重要になる.
それを証明するために,次の順序で式(1)の積分を行う.
-4pt
- コサイン(余弦関数)間の直交関係
- サイン(正弦関数)間の直交関係
- コサインとサインの間の直交関係
- 定数関数
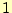 とコサインとの直交関係
とコサインとの直交関係
- 定数関数
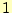 とサインの直交関係
とサインの直交関係
それでは直交関数系と成っていることを示そう.![]() と
と![]() を自然数として,最初にコサイン同士の積分の計算を行う.
を自然数として,最初にコサイン同士の積分の計算を行う.
同じことをサインの積に対して行う.
が得られる.サインとコサインの積は簡単で,
となる.最後に,定数関数
以上より,任意の関数![]() をフーリエ級数で展開するときの関数の集合
をフーリエ級数で展開するときの関数の集合
は直交関数系となっていることが分かる.
2.1.2 フーリエ係数の計算
周期これをフーリエ級数(Fourier series)と言い,自然現象の解析に大変役立つものである. 三角関数の係数
2.1.2.1 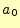 の計算
の計算
式(6)の両辺を区間
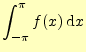 |
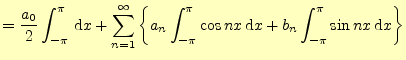 |
|
|
式(5)を使うと
| ||
| (7) | ||
これより,
となり,
この式をよく見ると,![]() は
は![]() の平均値となっている.電気回路では,この平均
値のことを直流成分と言う.
の平均値となっている.電気回路では,この平均
値のことを直流成分と言う.
2.1.2.2 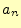 の計算
の計算
式(6)の両辺にこれより,
を計算することにより,
2.1.2.3 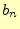 計算
計算
つぎに,式(6)の両辺にこれより,
を計算することにより,
2.1.3 具体的な周期関数
試験を受けるに際して,次のような周期関数をフーリエ級数で表せるようになること.
2.2 周期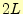 の場合
の場合
全く同じ議論が,周期となる.このような関数で展開する場合,
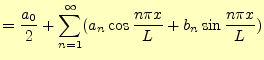 |
(13) | |
ただし,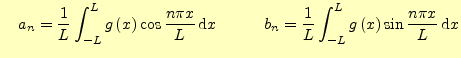 |
となる.これが,任意の周期
2.3 周期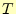 の場合
の場合
電気の問題でフーリエ級数を使う場合,横軸は| (14) |
に気を付けて,
となる.周期
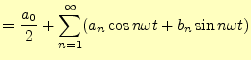 |
(15) | |
ただし,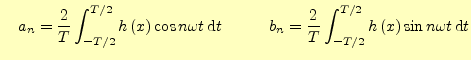 |
となる.
一般には,
![]() や
や
![]() を基本波と呼び,
を基本波と呼び,![]() の場合の
の場合の
![]() や
や
![]() を高調波と呼ぶ.
を高調波と呼ぶ.
2.4 偶関数と奇関数
偶関数や奇関数といった対称性を考えると,より次の積分の関係も得られる.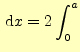 偶関数 偶関数 |
(16) |
この対称性を使うと,以下の結果が得られる.
- 周期関数
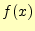 が偶関数の場合
が偶関数の場合
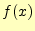
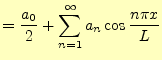
(17) 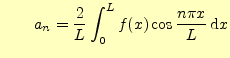
これをフーリエ余弦級数と呼ぶ. - 周期関数
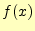 が奇関数の場合
が奇関数の場合
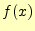
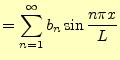
(18) 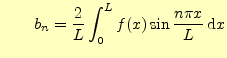
これをフーリエ正弦級数と呼ぶ.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年12月1日
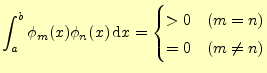
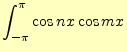
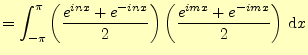
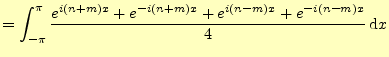
![$\displaystyle =\frac{1}{2}\int_{-\pi}^{\pi}\left[\cos(n+m)x+\cos(n-m)x\right]\,\mathrm{d}x$](img33.png)
![$\displaystyle =\begin{cases}\frac{1}{2}\left[\frac{\sin(n+m)x}{n+m}+x\right]_{-...
...n(n+m)x}{n+m}+\frac{\sin(n-m)x}{n-m}\right]_{-\pi}^{\pi} & (n\ne m) \end{cases}$](img34.png)
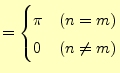
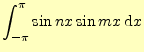
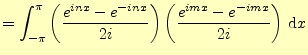
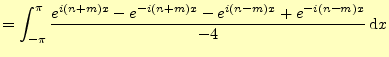
![$\displaystyle =-\frac{1}{2}\int_{-\pi}^{\pi}\left[\cos(n+m)x-\cos(n-m)x\right]\,\mathrm{d}x$](img39.png)
![$\displaystyle =\begin{cases}-\frac{1}{2}\left[\frac{\sin(n+m)x}{n+m}-x\right]_{...
...n(n+m)x}{n+m}-\frac{\sin(n-m)x}{n-m}\right]_{-\pi}^{\pi} & (n\ne m) \end{cases}$](img40.png)
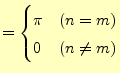
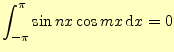
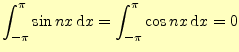
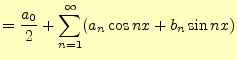
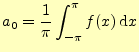
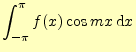
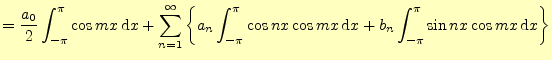
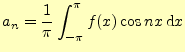
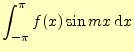
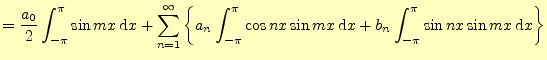
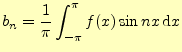
![\includegraphics[keepaspectratio, scale=1.0]{figure/rectangular.eps}](img92.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/triangle.eps}](img95.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/nokogiri.eps}](img98.png)