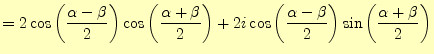2 テイラー展開から三角関数の諸公式
2.1 テイラー展開
2.1.1 任意のデータを冪級数で表現
| (6) |
には
2.1.2 任意の関数のテイラー展開
前節では,どんな任意のデータでも冪乗の関数で表現できることを示した.データの数が 非常に多くなって,無限までになったらどうなるだろうか?.データの数が無限というの は,データが連続するもの,すなわち関数と考えることができる.例えば,三角関数は無限 個のもし,ある関数が無限個のデータの集まりと考え,
と表すことができるとしよう.
任意の関数![]() が式(7)のように冪級数に展開できるならば,そ
の係数
が式(7)のように冪級数に展開できるならば,そ
の係数![]() をどうやって決めるのか?--という問題がのこる.有限個の場合のように,
連立方程式から係数を計算することはできない.無限次元の連立方程式など
解けないからである.そこで,連続な関数という性質を使う.元の式(7),お
よびその両辺を繰り返し微分すると次の式が得られる.
をどうやって決めるのか?--という問題がのこる.有限個の場合のように,
連立方程式から係数を計算することはできない.無限次元の連立方程式など
解けないからである.そこで,連続な関数という性質を使う.元の式(7),お
よびその両辺を繰り返し微分すると次の式が得られる.
| (8) | ||
| (9) | ||
| (10) | ||
| (11) | ||
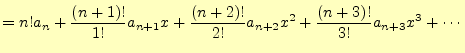 |
(12) |
これらの式で
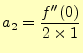 |
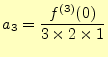 |
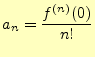 |
(13) |
と得られる.
となる.これで,任意の関数を冪級数で展開する方法が分かった2.このようにある関数を 冪球数で展開する方法をテイラー展開と言う.
式(14)は,不思議な式である.一般に,左辺の関数の定義域は
![]() と広い.それに対して,右辺の冪級数は
と広い.それに対して,右辺の冪級数は![]() の値のみできまる.無
限にひろがる関数が
の値のみできまる.無
限にひろがる関数が![]() のときの性質で決まる--という不思議なことになっている.
のときの性質で決まる--という不思議なことになっている.
まとめ(テイラー展開)
|
2.1.3 三角関数と指数関数のテイラー展開
先の説明では,どんな関数でも冪球数に展開できると言った.そこで,三角関数と指数関 数をテイラー展開3してみよう.
式(14)の![]() を
を![]() とすると,
とすると,
がえられる.いままで,三角関数は幾何学的な意味で使われてきた.幾何学的に考えた三 角関数の場合,任意の
でも,本当かなー--という疑問が湧く者もいるだろう.正直,私も信じられない.この
ような時,私はコンピューターを使って確かめることが多い.式(15)
の右辺を
![]() まで,展開の項数を変化さて
計算してみた.その結果を図2に示す.展開の項数が増加するごとに
まで,展開の項数を変化さて
計算してみた.その結果を図2に示す.展開の項数が増加するごとに![]() を正確に表していることが分かるであろう.これで,テイラー展開は正しいと信じた.
を正確に表していることが分かるであろう.これで,テイラー展開は正しいと信じた.
同じことを![]() で行うと,次の結果が得られる.
で行うと,次の結果が得られる.
指数関数![]() もテイラー展開できる.
もテイラー展開できる.
これらの三角関数と指数関数のテイラー展開の式から,それぞれの関数の値を解析的に計 算ができるようになる.いままで,三角関数は幾何学的に,指数関数は乗算の延長??のよ うに定義されていた.このような定義では,解析に値を計算することに困難をきたす.そ れに代わり,このテイラー展開の式がそれぞれの関数の定義と考えると,計算が格段に簡 単になる.このように定義しても,いままで使ってきた三角関数や指数関数の性質は失わ れない4.そこで, これからは三角関数と指数関数の定義として,テイラー展開の結果を使う.
まとめ(三角関数と指数関数テイラー展開)
|
2.2 オイラーの公式
三角関数と指数関数のテイラー展開の式(15)と(16), (17)はよく似ている.若干異なるが,虚数単位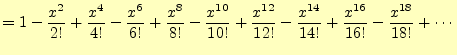 |
||
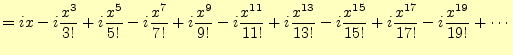 |
||
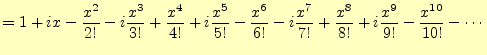 |
ますます,三角関数と指数関数が似てきた.これらより,
が得られる.これが,オイラーの公式と呼ばれるものである.虚数を介して,三角 関数と指数関数がこんなにも簡単な式で結ばれているのである.これは便宜的に記述した だけの式に見えるが,科学技術の問題を考えるときに極めて有用である.これを使うとや やこしい計算をすること無く,様々な問題が解ける.諸君はできるだけオイラーの公式を 利用せよ.
オイラーの公式から,
と書くこともできる.
もともと,三角関数は幾何学的に定義された.それに対して,指数関数は解析的に定 義された.そして,虚数は方程式を解くために導入された.これら,勝手に定義されたも のが,こんな単純な式で関係づけられるのは驚きである.
2.3 三角関数の諸公式
オイラーの公式を使うと,この節で示すように三角関数に関する公式が簡単に得られる. この単純な方法を憶えておくと,後々,便利である.これだけでもオイラーの公式の御利 益が分かるだろう.
2.3.0.1 加法定理
| (20) |
となる.両辺が等しいということは,実部と虚部が等しいということである.したがって,
| (21) | ||
| (22) |
が得られる.これは,三角関数の加法定理そのものである.
2.3.0.2 倍角の公式
| (23) |
となる.これもまた,実数部と虚数部の各々が等しいので,
を得る.これは倍角の公式である.同様の手順で,
| (26) | ||
| (27) |
3倍角の公式
| (28) | ||
| (29) |
が簡単に得られる.
2.3.0.3 半角の公式
式(24)を使っても簡単に求められる.式 (19)から計算することもできる.![$\displaystyle =\left[\frac{e^{i\frac{x}{2}}-e^{i\frac{x}{2}}}{2i}\right]^2$](img97.png) |
(30) | |
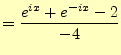 |
(31) | |
| (32) |
同じことをすれば,余弦に関する公式 も得られる.
| (33) |
2.3.0.4 積を和に変換する公式
加法定理を上手に使えば,三角関数の和を積に変換する公式は得られる.次のようにして 計算することもできる.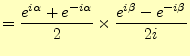 |
||
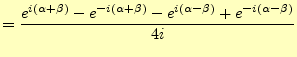 |
||
![$\displaystyle =\frac{1}{2}\left[ \frac{e^{i(\alpha+\beta)}-e^{-i(\alpha+\beta)}}{2i} -\frac{e^{i(\alpha-\beta)}-e^{-i(\alpha-\beta)}}{2i}\right]$](img104.png) |
||
| (34) |
積を和に変換する残りの公式
| (35) | ||
| (36) | ||
| (37) |
も同様に導くことができる.良い練習問題なので,諸君は自力で導いてみよ.
2.3.0.5 積を和に変換する公式
これは,ちょっと変わっていて,次のようにする.ところで,この式の右辺は,次のように書くこともできる.
もちろん,式(38)と(39)の両式の右辺は等しい.したがっ て,各々の実数部と虚数部が等しくなり,
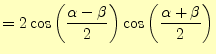 |
(40) | |
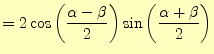 |
(41) |
が得られる.これは,三角関数の和を積に直す公式である.同様にして,
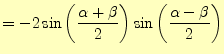 |
(42) | |
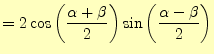 |
(43) |
が得られる.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年10月27日
![\includegraphics[keepaspectratio, scale=1.0]{program/pow10.eps}](img14.png)
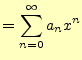
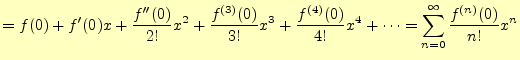
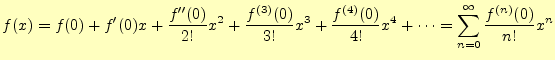
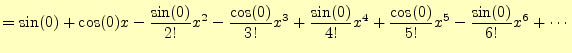
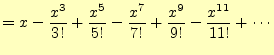
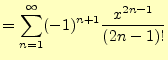
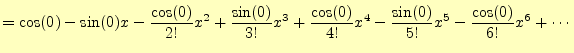
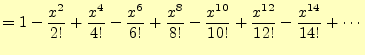
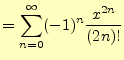
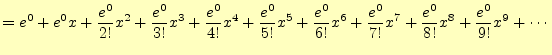
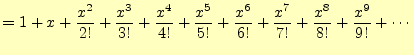
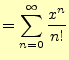
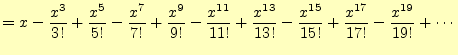
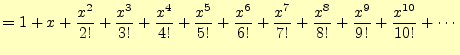
![\includegraphics[keepaspectratio, scale=1.0]{program/sin.eps}](img61.png)
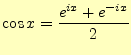
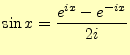
![$\displaystyle =\left[\cos\left(\frac{\alpha+\beta}{2}\right)+i\sin\left(\frac{\alpha+\beta}{2}\right)\right]$](img112.png)
![$\displaystyle \qquad\qquad\times\left[\cos\left(\frac{\alpha-\beta}{2}\right)+i...
...t(\frac{\alpha-\beta}{2}\right)-i\sin\left(\frac{\alpha-\beta}{2}\right)\right]$](img113.png)
![$\displaystyle =2\cos\left(\frac{\alpha-\beta}{2}\right)\left[\cos\left(\frac{\alpha+\beta}{2}\right)+i\sin\left(\frac{\alpha+\beta}{2}\right)\right]$](img114.png)