1 前回の復習と本日の学習内容

1.1 前回の内容

前回は，これまでの学習の確認試験を行った．統計データについては，後日報告する．

1.2 本日の内容

最初に断っておくが，私は数学の専門家ではない．しかし，数学をよく使いいろいろな場 面でお世話になっている．そのため，厳密な証明よりも実際の場面で使えるように直感的 に理解することの方を重要視している．この講義では，分かり難く退屈な証明よりも感覚的 に理解することを目指す．その方が実際の科学技術の問題を数学を使って解決するときに 役に立つ．ただ，厳密な数学の証明が不要というわけではない．それは，数学の講義に任 せることにする．

本日は，三角関数に関する諸公式をオイラーの公式(Euler's formula)より簡単に導く方 法を示す．この講義のメインテーマであるフーリェ解析(Fourier analysis)では三角関数 に係わる計算が多い．三角関数の性質が分かっていないと，計算ができなくなる．そこで， 本日の講義では，以下のような順序で三角関数の諸々の定理を導く．

1. 任意の関数を冪級数(power series)に展開するテイラー展開(Taylor expansion)，ここではその特別な場合のマクローリン展開(Maclaurin's expansion)を示す．テイラー展開を用いると，任意の関数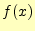$f(x)$は

   $$f(x) =f(0)+f^\prime(0)x+\frac{f^{\prime\prime}(0)}{2!}x^2+ \frac{f^{(3)}(0)}{3!}x^3+\cdots$$

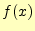
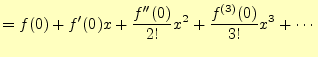
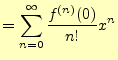
   $$=\sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n$$ (1)

   
   
   と表すことができる．
2. 三角関数や指数関数もテイラー展開可能である．それらを，冪級数で表すと

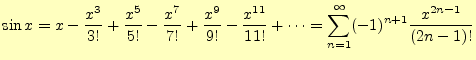
   $$\sin x = x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+ \frac{x^... ...frac{x^{11}}{11!}+\cdots =\sum_{n=1}^{\infty}(-1)^{n+1}\frac{x^{2n-1}}{(2n-1)!}$$ (2)

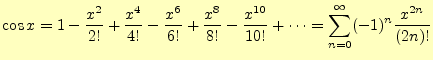
   $$\cos x = 1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+ \frac{x^8}{8!}-\frac{x^{10}}{10!}+\cdots =\sum_{n=0}^{\infty}(-1)^{n}\frac{x^{2n}}{(2n)!}$$ (3)

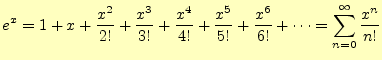
   $$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+ \frac{x^5}{5!}+\frac{x^6}{6!}+\cdots =\sum_{n=0}^{\infty}\frac{x^n}{n!}$$ (4)

   
   
   となる．これら，オイラーの公式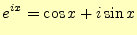

   $$e^{ix}=\cos x+i\sin x$$ (5)

   
   
   を導くことができる．
3. オイラーの公式から，三角関数に関する諸々の定理--加法定理や倍角の公式など-- をしめす．

これを理解すると，三角関数に係わるいろいろな問題が簡単に計算できるようになる．そ ればかりではなく，来年学習する複素関数などの学習にもスムーズに移行できるであろう． さらに，数学のみならず，電気に関係する問題も簡単に計算できるようになる．

ホームページ: Yamamoto's laboratory
著者: 山本昌志