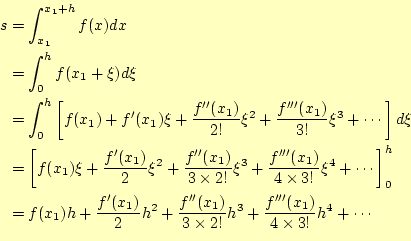2 台形公式
2.1 台形公式の求め方
定積分、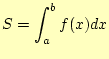 |
(3) |
の近似値を数値計算で求めることを考える。積分の計算は、先に示したように面積の計算 であるから、図2のように台形の面積の和で近似ができるであ ろう。積分の範囲
となる。これが数値積分の台形公式である。なんのことはない、積分を台形の面積に置き 換えているだけである。
2.2 台形公式の誤差について
台形公式による数値積分では、分割数
まずは、式4のある一つの台形の面積と実際の積分の値を比較する。台
形の面積![]() は、台形公式より、
は、台形公式より、
となる。これを実際の積分
と比較することにする。これら2つの式の形がぜんぜん違うので比較できないと考えるか もしれないが、このような場合の常套手段がある。このようなときには、テーラー展開を すれば良いのである。式(5)を
となる。これが台形の面積のテイラー展開である。一方、積分の 式(6)もテイラー展開する。これは、
となる。この2つの式(7)と ( 8)が台形での近似と まっとうに積分を行ったときのテイラー展 開を表す。これらの式を比べると、刻み巾
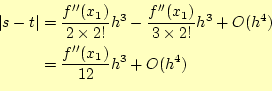 |
と表せる。即ち、積分を台形で近似したひとつの区間の誤差は、刻み幅の
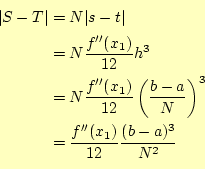 |
となる。要するに積分の誤差は、分割数
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成17年1月25日
![\begin{equation*}\begin{aligned}T&=h\frac{f(a)+f(a+h)}{2}+ h\frac{f(a+h)+f(a+2h)...
...{2}\sum_{j=0}^{N-1}\left[f(a+jh)+f(a+(j+1)h)\right] \end{aligned}\end{equation*}](img8.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/trapezoidal.eps}](img9.png)
![$\displaystyle t=\frac{h}{2}[f(x_1)+f(x_1+h)]$](img11.png)
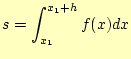
![\begin{equation*}\begin{aligned}t&=\frac{h}{2}[f(x_1)+f(x_1+h)] &=\frac{h}{2}\...
...c{f^{\prime\prime\prime}(x_1)}{2\times3!}h^4+\cdots \end{aligned}\end{equation*}](img14.png)