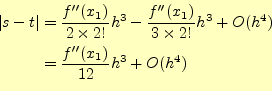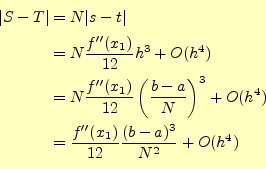定積分、
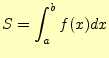 |
(3) |
の近似値を数値計算で求めることを考える。積分の計算は、先に示し
たように面積の計算であるから、図2のように台形
の面積の和で近似ができるであろう。積分の範囲![$ [a,b]$](img6.png) を
を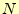 等分した台形で
近似した面積Tは、
等分した台形で
近似した面積Tは、
となる。これが数値積分の台形公式である。なんのことはない、積分を台形の
面積に置き換えているだけである。
台形公式による数値積分では、分割数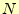 を大きくするとその誤差は小さくな
ることは直感で分かる。それでは、分割数を増やしていくとどのように精度が
良くなるのか考えてみよう。
を大きくするとその誤差は小さくな
ることは直感で分かる。それでは、分割数を増やしていくとどのように精度が
良くなるのか考えてみよう。
まずは、式4のある一つの台形の面積と実際の積分の値を比
較する。台形の面積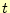 は、台形公式より、
は、台形公式より、
となる。これを実際の積分
と比較することにする。これら2つの式の形がぜんぜん違うので比較できない
と考えるかもしれないが、このような場合の常套手段がある。このようなとき
には、テーラー展開をすれば良いのである。式(5)を
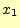 の周りで、テイラー展開すると
の周りで、テイラー展開すると
となる。これが台形の面積のテイラー展開である。一方、積分の式(6)もテイラー展開する。これは、
となる。この2つの式(7)と(
8)が台形での近似とまっとうに積
分を行ったときのテイラー展開を表す。これらの式を比べると、刻み巾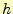 の2
次まで一致している。異なるのは3次以降で、積分の誤差は、
の2
次まで一致している。異なるのは3次以降で、積分の誤差は、
と表せる。
これは、一つの台形近似の積分の誤差で、全てトータルの誤差は、
となる。要するに積分の誤差は、分割数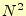 に反比例する。分割数を10倍に
すれば、積分の誤差は1/100になるわけである。
に反比例する。分割数を10倍に
すれば、積分の誤差は1/100になるわけである。
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年8月21日
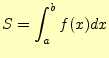
![]() は、台形公式より、
は、台形公式より、