1 はじめに

数学の授業で学習したように、どんな複雑な関数でも微分は可能である。一方、 積分となるとそうはいかない。積分の学習では、どのようにして積分を行うか といういろいろなテクニックを学んだはずである。微分に比べれば、圧倒的に 計算が難しいことも経験済みであろう。

例えば、ガウス分布を表す以下の関数を考える。

$$f(x)=e^{-x^2}$$ (1)

この関数の微分すること(導関数)は、簡単で

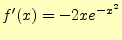$$f^\prime(x)=-2xe^{-x^2}$$ (2)

となることは説明の必要がないであろう。今まで学習してきたように、初等関 数で表すことができる関数の微分は、初等関数で表現できるのである。要する に微分(導関数)の値を求めたいときには、人間が実際に微分をして、初等関数 を計算すればよいのである。

一方、積分となるとそうはいかない。先の式 (1)の不定積分を初等関数で表すことが できない。初等関数からできた関数であろうとも、不定積分は初等関数の範囲 を超えることがある。だからといって、定積分の値(数値)が不定というわけでは ない。

いろいろ計算をしていると、不定積分はできないが、定積分の値が必要な場合 がしばしば訪れる。そのときに、ここで学習する定積分を数値計算で求めるテ クニックが使われる。

定積分は、図1に示すように面積の計算になる。したがっ て、直感的にわかりやすく、アルキメデスの時代からあった。一方、微分法は ニュートンの時代とすると、およそ2000年の開きがあるのである。

図 1: 定積分と面積

ホームページ: Yamamoto's laboratory
著者: 山本昌志