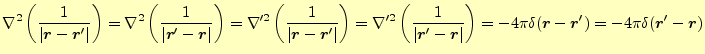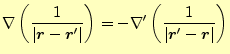2 ディラックのデルタ関数
2.1 デルタ関数のイメージ
大きさの無い電荷や,作用している時間がゼロの衝撃力等を表したいことがある.このよ うな場合,ディラックのデルタ関数である.これを使うと,都合良く電荷密度を表すことができるが,それはこれからの講義 内容である.しかし,衝撃力を表すのにうってつけであることは理解できるであろう.
いろいろな![]() 関数が考えられる.その中でも,直感的にもっともわかり易いの
は,図2のようなものである.この図の
関数が考えられる.その中でも,直感的にもっともわかり易いの
は,図2のようなものである.この図の
![]() の極
限をデルタ関数とする.デルタ関数の定義である式(4)や
(5)を満足していることが分かるだろう.
の極
限をデルタ関数とする.デルタ関数の定義である式(4)や
(5)を満足していることが分かるだろう.
2.2 さまざまな積分とデルタ関数の定義
このデルタ関数の重要な関係式を示しておこう.2.2.1 さまざまな積分
2.2.1.1 積分1
まずは,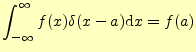 |
(6) |
である.これは,図2をデルタ関数として,次のようにして計算できる.
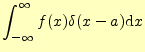 |
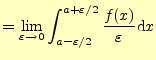 |
|
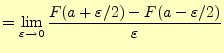 |
||
| (7) |
2.2.1.2 積分2
先ほどの積分は直感的に理解できるであろう.それに対して,次はちょっと難しい.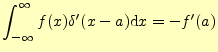 |
(8) |
これは,次のように,部分積分を使って計算する.
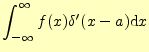 |
![$\displaystyle =\Bigl[f(x)\delta(x)\Bigr]_{-\infty}^{\infty}- \int_{-\infty}^{\infty}f^\prime(x)\delta(x-a)\mathrm{d}x$](img25.png) |
|
| (9) |
2.2.1.3 フーリェ変換
これは,計算するまでもなく.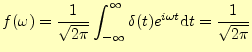 |
(10) |
となる.これは,非常に短いパルスのノイズは,広帯域の周波数成分があることを示して いる.短パルスのノイズは広帯域なので,フィルターで取り除くことは難しい.
2.2.1.4 三次元
一次元とほとんど同じで,三次元に拡張することができる.基本的な 性質は,である.同様に積分は,
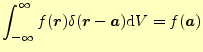 |
(12) |
となる.これらの振舞いは,一次元とほぼ同じなので,細かい説明はしない.
2.2.2 デルタ関数の定義
これまで,デルタ関数のいろいろな性質を見てきた.いったい,デルタ関数はどのように 定義すればよいのだろうか? これまででもっとも一般的な--デルタ関数の性質に関して 最も広い範囲をカバーする--式は,である.式(4)や式(5)に代わり,これ をデルタ関数の定義3としよう.これが関数の定義としてふさわしいかどうか--という議 論もあるだろう.ちゃんとした定義は数学者に考えてもらえばよく,我々はこれで十分で ある.物理的な内容を便利に表すことができるからである.
2.3 ラプラス演算子との関係
2.3.1 特異点が原点の場合
つぎにラプラス演算子との関係を示す.後に重要となる公式で,電磁気学ではとくに有用 である.もっとも重要な公式は,である.
これを証明するためには,ちょっと頑張らなくてはならない.まずは,左辺であるが,以 前の課題に出したように
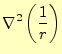 |
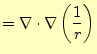 |
|
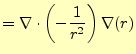 |
||
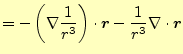 |
||
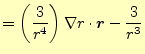 |
||
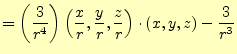 |
||
| (16) |
となる.これで,式(11)の原点(
原点
![]() での値を計算するために,式(15)の左辺を体積
分する.図3のように,原点を含まない場合,
での値を計算するために,式(15)の左辺を体積
分する.図3のように,原点を含まない場合,
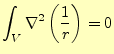 |
(17) |
となる.いまのところ,この結果には面白いところはない.値がゼロのところを積分して, ゼロが得られただけである.
図4のように積分領域に原点が含まれる場合,大事な結果が得ら れる.原点は特異点なので,そのまま積分はできない.そこで,原点を含まない領域で積 分をする.複素関数論でコーシーの積分公式を導くのとと同じ方法である.このようにすると,積分領域に 原点が含まれなくなり,積分の値はゼロとなる.そして,連結部を非常に小さくとり,体 体積分を面積分に直すガウスの定理を使うと,式(15)の左辺の体 積分は
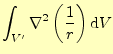 |
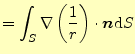 |
|
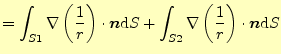 |
||
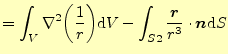 |
(18) |
となる.ここで,
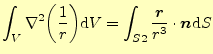 |
(19) |
となる.これで原点を含んだ領域
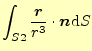 |
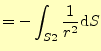 |
|
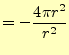 |
||
| (20) |
となる.従って,
となる.これと,式(16)とデルタ関数の定義から,
とかける.これで,式(15)が証明できた.これは,今後しばしばお 目にかかる式である.ただし,積分を行うときに重要な意味があることを忘れてはならな い.
ところで,式(21)は不思議な式である.被積分関数は原点を除 いてゼロである.原点の値は不定であるが,積分を行うとちゃんとした値になる.
2.3.2 特異点が任意の位置
2.3.2.1 ラプラス演算子が
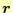 に作用する場合
に作用する場合
次に被積分関数の特異点の位置を変えてみよう.先ほどは原点に特異点があったが,ここ
では位置
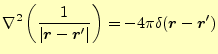 |
(23) |
となる.このとき,
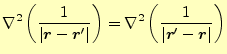 |
(24) |
が得られる.
また,デルタ関数の性質より,
![]() である.デルタ関数の
定義の式(13)に関する矛盾はない.次に式
(14)に関しては,実際に計算してみる.途中,変数変換
である.デルタ関数の
定義の式(13)に関する矛盾はない.次に式
(14)に関しては,実際に計算してみる.途中,変数変換
![]() を使うと,
を使うと,
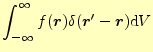 |
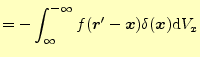 |
|
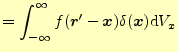 |
||
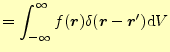 |
(25) |
となる.これから,
ここでの結果をまとめると,次のようになる.
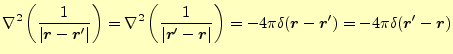 |
(26) |
2.3.2.2 ラプラス演算子が
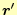 に作用する場合
に作用する場合
次に,
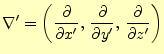 |
(27) |
を導入する.先ほどの結果から,明らかに
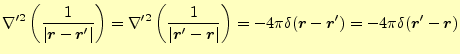 |
(28) |
の関係がある.すべての変数を,プライムの付くものと付かないものを入れ替えただけで ある.
2.3.2.3 まとめ
これらの結果をまとめると,となる.プライムが付くものと付かないものを入れ替えてよいのである.これは後々,か なり便利に使える.
この入れ替えができる演算は限られており,次のような場合は入れ替えができないことに 注意が必要だ.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年7月5日
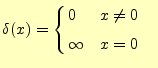
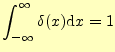
![\includegraphics[keepaspectratio, scale=1.0]{figure/delta_func.eps}](img14.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/pulse.eps}](img17.png)
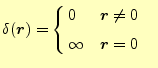
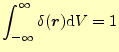
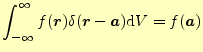
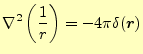
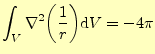
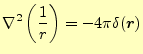
![\includegraphics[keepaspectratio, scale=0.7]{figure/soto.eps}](img65.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/laplace_delta.eps}](img66.png)