4 ローレンツの力
4.1 荷電粒子に働く力
電場中の荷電粒子は,| (35) |
という力を受ける.これが電場の定義と考えて良い.次に考えるのは磁場中であるが,我々 はアンペールの力の法則しか知らない.これから導くことにする.ある断面を
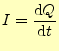 |
(36) |
となる.導線の中の電流を担う電荷の単位長さ当たりの密度を
| (37) |
となる.この電流が流れている導線(長さ
| (38) |
という力をうける.この中に,
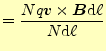 |
||
| (39) |
となる.これが磁場中で,荷電粒子が受ける力を示す.電場と磁場の力を合わせて,
| (40) |
となる.これが,電磁場中の荷電粒子が受ける力で,ローレンツ力と呼ばれる.
4.2 一様な静磁場内の粒子の運動
一様な磁場内での荷電粒子の運動を考える.ローレンツ力より,運動方程式は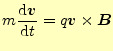 |
(41) |
となる.力は磁場と速度の双方の直角方向に働いている.特に速度の直角方向に働いてい ることが重要である.速度の直角方向に力を受けるので,粒子は磁場からエネル ギーを受けることはない.エネルギーは,力と移動方向の内積で,この場合
|
|
||
| (42) |
となる.従って,運動エネルギーは一定で,速度の大きさも変化しない.もう少し想像力 を働かせると,,荷電粒子は磁場に巻き付くようにらせんに運動することがわかる.ちゃ んと計算したければ,円筒座標系を使って計算すれば,このことは直ちに分かるであろう.
次に,粒子の速度が磁場と垂直の場合を考える.この場合,らせんは進むことが無く,粒 子は平面内を等速円運動する.円筒座標系の運動方程式は,
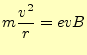 |
(43) |
となる.速度
| (44) |
となる.速度が大きくなれば回転半径は大きくなり,磁場を強くすれば回転半径は小さく なる.また,角速度は
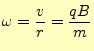 |
(45) |
となる.角速度は,粒子の速度に依存しないで一定の値となる.この
このように一様な磁場では,粒子の運動エネルギーに関係なく,一定の角速度で粒子は回 転する.サイクロトロンと呼ばれる加速器は,この原理を利用している.粒子の回転周波 数に応じた電場により加速して,高エネルギーの粒子を得る装置である.ただし,粒子の エネルギーが大きくなると,粒子の質量が大きくなり,回転周波数が変化する.そうする と加速ができなくなり,サイクロトロンの限界となる.
また,粒子が完全にいつも磁場と垂直の速度を持つことはあり得ない.ほんのちょっとの 角度を持っても,らせん運動が発生して,上下の磁極の衝突する.これを防ぐために,実 際のサイクロトロンでは上下方向に安定な運動するようにしている.これは,完全に一様 な磁場を用いるのではなく,少し変化させている.興味がある者は調べよ.
4.3 ローレンツ力のパラドックス
図10で示す2つの座標系での磁場による力を考える.
この矛盾を解決するためには,特殊相対性理論を使って説明する必要がある.ここでは,
結論を述べるにとどめる.
![]() 座標系では,電場と磁場の両方が観測さ
れ,それぞれによる力の和はゼロとなる.従って,2つの座標系での物体の運動は同一に
なる.
座標系では,電場と磁場の両方が観測さ
れ,それぞれによる力の和はゼロとなる.従って,2つの座標系での物体の運動は同一に
なる.
4.4 ローレンツ力と作用・反作用の法則
2個の質点がお互いに及ぼし合う力は,大きさが等しく,かつ方向が反対方向である.こ れを作用・反作用の法則という2.この作用・反作用の法則が成り立つと,この系の運動量が保存され る.この辺は力学の基礎なので,忘れた者は各自復習せよ.ここでは,ローレンツ力にお いても,作用と反作用の法則が成り立つか調べる.図11のように2つの質点がお互いに作用を及ぼしあって,運動している ような状況を考える.明らかに電場による力は,作用反作用の法則を満たしている.一方, 磁場の方はそんなに簡単ではない.一番手っ取り早いのは,作用・反作用の法則が成立し ない例を示すことである.教科書の図6.5がその例になっている.
結論は電磁場の運動量も考慮に入れると,作用・反作用の法則は成り立っているのである. この辺を詳細に述べる時間はない.しかし,作用・反作用の法則はいつでも成り立ってい るのである.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年7月26日
![\includegraphics[keepaspectratio, scale=1.0]{figure/Lolentz_paradox.eps}](img164.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/shitten2.eps}](img165.png)