2 ビオ-サバールの法則
2.1 クーロンの法則とビオ-サバールの法則
静電場の場合,微少体積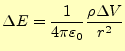 |
(1) |
となった.これに対応する静磁場の式がビオ-サバールの法則である.電流
となる.図1にこれらの位置関係を示す.この微小磁場
- 大きさは,式(2)の示すとおりである.
- 観測点の位置ベクトル
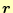 と微少電流ベクトル
と微少電流ベクトル
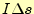 の
両方に垂直な方向を向いている.
の
両方に垂直な方向を向いている.
ちょっとこれらの式は方向を指定することが不可能なので,それを含めた正確なベクトル で表現する.ベクトルを用いて表現すると,図など書かなくても式が全てを語っている.それぞれは,
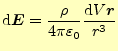 |
(3) | |
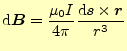 |
(4) |
となる.ただし,微少電流や微少電荷を座標原点に置いている.この後者をビオ-サバー ルの法則と言う.
一般的なクーロンの法則とビオ-サバールの法則は,
となり,両者の対応が良い.こうなると,
2.2 ビオ-サバールの法則について注意
式(5)のクーロンの法則は物理的なイメージを思い浮かべることができ る.そして,実際にその物理的な状態--図2--はある.それに対して, ビオ-サバールの法則が述べているような物理的な状態--図3--は, 静磁場ではありえない.電流が途中で途切れており,電荷保存則を満足していない.ある 電荷が運動している状態のスナップショットを考えれば,図3の状態 は可能である.そうした場合,もはや静電場とは言えず,式(6)は 成り立たない.運動する電荷が作る電磁場は特殊相対性理論を使って導くことになる.こ の話は非常に面白いが,講義の時間の都合で話せない.ビオ-サバールの法則は静電場について述べているが,実際にそのような物理的な状態は 不可能である.そんな法則に意味があるのか?--と言う疑問が湧くだろう.ビオ-サバー ルの法則の積分形は物理的にありえる.そして,式(6)の積分形
は常に静磁場では正しいのである.磁場を求めたければ,全ての領域にわたって,電流密 度を積分すればよいのである.
理論を作る場合,ビオ-サバールの法則の式(6)から出発すると, すっきりする.静電場と同じように straight forward に理論が展開できる.ここでの講 義では実験事実からはじめたが,ジャクソンの電磁気学 [1]で はビオ-サバールから出発している.
2.3 ビオ-サバールの法則の導出
このビオ-サバールの法則は,特殊相対性理論を用いて導くのが本来の姿と思われる--と 昨年は説明した.それでも,ビオ-サバールの法則の完全な形を得るのは難しいかもしれ ない.時間があるときにトライしてみよう....そこで,静磁場の知識のみですむ教科書と同じ 説明をする.正直に言うと,このような説明方法があるとは知らなかった.さすが,砂川 重信先生である.今まで学習してきた磁場は,全て端が無い電流により作られる.すなわち,無限に長い電 線や閉じた電線である.ビオサバールの法則を見ると,微少区間の電流を取り扱っている ので,端が存在する.そのような電流を考えると,積分型のアンペールの法則が成り立た なくなる.これは,電流が保存されていないからである.
電流が保存された系で微少電流を考えるために,教科書では,微少電線の両端で発散と収 束を考えている.このようにする限り,電流は保存され,積分型のアンペールの法則が成 立する.また,これらの微少電流を足しあわせることにより,無限に長い電流や閉じた電 流を考えることができる.砂川先生がこのようなことを考えた理由は,次のようなことか らであろう.
- ビオ-サバールの法則が成り立つ,物理的な例を示したい.ただし,電流の保存則
を満たさなくてはならない.そのためには,両端から電流が出入りするがそれら
が磁場を作らなければ良い.電流が流れるが磁場を作らない.さあ,どうするか?.
立体角
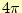 に等方に放射状に電流が流れれば良い.放射状の電流は磁場を作ら
ない.
に等方に放射状に電流が流れれば良い.放射状の電流は磁場を作ら
ない.
図4のような電流を考える.これについて,アンペールの法 則を適用して,ビオ-サバールの法則を導く.
それでは,このような微少電流からビオ-サバールの法則が成立するか,調べることにす
る.教科書の図5.9(a)に示している磁場
![]() を求める.そのために,積分形
のアンペールの法則
を求める.そのために,積分形
のアンペールの法則
を使う.ある閉じた面の縁の磁場の線積分は,内部の電流密度の面積分に等しい.もっと 簡単に言うと,磁場を線積分したら,そこの面を流れる電流に等しいと言っているのであ る.これを利用して磁場を求めようと言うのである.ビオ-サバールの法則を考えるため に,積分を行う範囲は,教科書の通り,円の一部を切り取った範 囲が適当である.この部分では,電流は一定である.なぜならば,微少電線の端では,球状に電 流が発散及び収束しており,この部分球の表面はその端から等距離にある.従って,ここ での電流密度は,
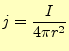 |
(9) |
となる.また,対称性から,磁場の大きさも一定
アンペールの法則,式(8)を用いて磁場![]() を計算することにな
るが,この左辺は簡単で
を計算することにな
るが,この左辺は簡単で
となる.
次に,式(8)の右辺を考えることにする.この右辺は,積分領域の
電流のを表している.ここでの,積分を行う部分の電流密度は一定で,
![]() と分かっている.したがって,積分領域の面積さえ分かれば,電流は計算でき,右
辺の値が分かることになる.教科書の図5.9(b)の帯状の微少区間の面積は,
と分かっている.したがって,積分領域の面積さえ分かれば,電流は計算でき,右
辺の値が分かることになる.教科書の図5.9(b)の帯状の微少区間の面積は,
| (11) |
となる.従って全ての面積は,区間
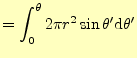 |
||
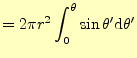 |
||
| (12) |
と求められる.従って,微少電線のAから流出する電流の総量は,この面積に電流密度を かければ求められ,
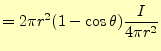 |
||
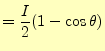 |
(13) |
となる.これは,距離に関係なく,角度のみに依存する.電流は保存され,球状に放出さ れるので当たり前のことである.
次に,同じ縁を持つ積分領域で教科書の図5.9のB点から吸収される電流を計算する.先の A点の放出電流の式が使える.異なるところは,角度のみである.したがって,B点への吸 収電流はとなる.
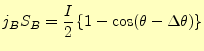 |
(14) |
A点の放出電流と,B点の吸収電流をあわせたものがトータルの電流で,
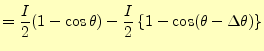 |
||
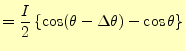 |
||
|
|
||
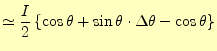 |
||
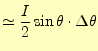 |
(15) |
となる.したがって,円
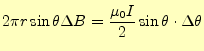 |
(16) |
となる.したがって,微小磁場は
となる.ビオ-サバールの法則まで,後一歩である.そのためには,
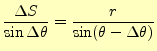 |
(18) |
から,
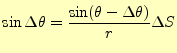 |
(19) |
が導かれる.
となる.
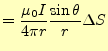 |
||
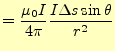 |
(21) |
となる.これがビオ-サバールの法則である.微少電流が作る微小磁場を表している.
もっと一般的な座標で書くと,
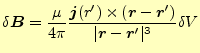 |
(22) |
となる.ここで,
2.4 円電流が作る静磁場
問題のコイルの1個が軸上に作る磁場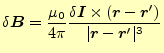 |
(23) |
から計算できる.これから,その磁場は図7 の右の絵のようになる.軸上の磁場
図から分かるように,微小磁場
![]() は軸の垂直成分もある.しかし,
これは,コイル1週にわたって足し合わせると,ゼロになる.コイル1周にわたっ
て合計すると,残るのは軸上の成分のみである.コイルの軸上の成分は,
は軸の垂直成分もある.しかし,
これは,コイル1週にわたって足し合わせると,ゼロになる.コイル1周にわたっ
て合計すると,残るのは軸上の成分のみである.コイルの軸上の成分は,
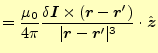 |
||
|
|
||
|
|
||
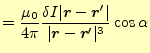 |
||
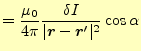 |
||
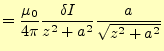 |
||
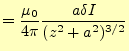 |
(24) |
となる.これをコイルの全ての電流で積分することになるが,
となる.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年7月26日
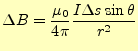
![\includegraphics[keepaspectratio, scale=1.0]{figure/BiotSavart_coil.eps}](img9.png)
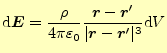
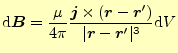
![\includegraphics[keepaspectratio, scale=1.0]{figure/Columb.eps}](img16.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/BiotSavart.eps}](img17.png)
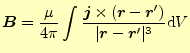
![\includegraphics[keepaspectratio, scale=1.0]{figure/dI_conserv_current.eps}](img20.png)
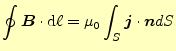
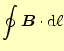
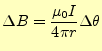
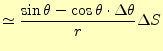
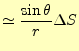
![\includegraphics[keepaspectratio, scale=1.0]{figure/theorem_sin.eps}](img62.png)
![\includegraphics[keepaspectratio, scale=0.8]{figure/dB_by_dj.eps}](img66.png)
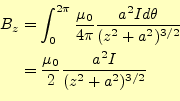
![\includegraphics[keepaspectratio, scale=1.0]{figure/OneTurn_coil.eps}](img85.png)