3 静電ポテンシャルとポアッソン方程式
3.1 最も有用な静電場の計算方法
電場
それでは,スカラー場が満たす方程式を考えよう.復習で示した式
(11)のように,スカラー場の勾配が電場,
![]() となる.これは,静電場をあらわす式(6),すなわち
となる.これは,静電場をあらわす式(6),すなわち
![]() を自動的に満足する.勾配の回転はゼロというベクトル恒等式
の示すとおりである.従って,残りは式(5),
を自動的に満足する.勾配の回転はゼロというベクトル恒等式
の示すとおりである.従って,残りは式(5),
![]() である.これを,満足させるためには,
である.これを,満足させるためには,
| (14) |
とすればよい.したがって,スカラーポテンシャルをあらわす微分方程式は
となる.この式を「ポアソン方程式」と言う.また,領域に電荷がない場合は
となり,これを「ラプラス方程式」と言う.静電場の場合,一般的にはポア ソン方程式で,電荷が無い特別な場合「ラプラス方程式」となる.
ポアソン方程式(15)は,スカラーの方程式なので解きやすい. 解きやすいといっても,これを直接計算するのは,そんなに易しいことではない.
計算はそんなに簡単ではないが,既にこの方程式の解は分かっている.先週,示したとお り
が解である.これが,ポアソン方程式(15)の解である.無限遠を基 準(
それでは,微分方程式(15)をどうやって解くと言うのだ.式 17の問題点は,積分範囲が無限と言うことである.ブラウン 管の電子銃の電場を計算するために,全宇宙の電荷を計算することになる.原理的に正し いが,そんなのはナンセンス.そこで,実際には有限な領域のみを計算対象とする.そし て,その領域の端--境界--でのポテンシャルに条件を与える.境界条件を与えて,内部 でのみポアソン方程式を計算する.具体的な計算方法は,時間がないので述べないが,
- 鏡像法
- 直交関数による展開
- 等角写像を用いる方法.これ,複素関数論の講義で学習した??.この方法は結構 面白いし,役に立つ.
- 差分法.これについては,5年生の計算機応用の講義で示した.
- 境界要素法
- 有限要素法
ポテンシャルが分かるとなにがうれしいか?.それは,ポテンシャルはそれだけでも電圧 という物理的な意味がある.それだけでもうれしいが,それを微分することにより電場も 求められるのである.ポテンシャルが分かると静電場の問題は解けたと言える.
3.2 電気双極子
この計算はちょっと退屈だが,ポテンシャルを使って計算することの利点がはっきりする ので,説明しておく.ポテンシャルから電場を計算する良い例である.図3のように,電荷量の絶対値は等しいが符号が異なる2つの電 荷が近距離にあるようなものを電気双極子と言う.この電気双極子が作る電場を求めたい. このような場を求める場合,ポテンシャルが大いに役立つ.
図3の![]() 点でのポテンシャルを計算する.ただし,
点でのポテンシャルを計算する.ただし,
![]() とする2.式
(17)で示したように,各々の電荷が作るポテンシャルの和と
なる.
とする2.式
(17)で示したように,各々の電荷が作るポテンシャルの和と
なる.
![$\displaystyle =\frac{q}{4\pi\varepsilon_0}\left[\frac{1}{r_1}-\frac{1}{r_2}\right]$](img52.png) |
||
| 余弦定理より | ||
![$\displaystyle =\frac{q}{4\pi\varepsilon_0}\left[\frac{1}{\sqrt{r^2-\left(\frac{...
...eta}}-\frac{1}{\sqrt{r^2-\left(\frac{s}{2}\right)^2-rs\cos(\pi-\theta)}}\right]$](img53.png) |
||
![$\displaystyle =\frac{q}{4\pi\varepsilon_0r}\left[\frac{1}{\sqrt{1-\left(\frac{s...
...a}}-\frac{1}{\sqrt{1-\left(\frac{s}{2r}\right)^2+\frac{s}{r}\cos\theta}}\right]$](img54.png) |
(18) |
ここで,
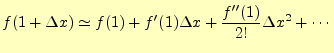 |
(19) |
を行う.これを使って,式18の
| (20) |
となる.これを利用すると,
| (21) |
となる.ここで,双極子モーメント
| (22) |
と定義する.すると,双極子が作るポテンシャルは,
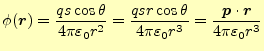 |
(23) |
と書きあらわせる.
ポテンシャルが求まった.残りの問題は,これを微分して電場に直すことである.
![$\displaystyle =-\frac{1}{4\pi\varepsilon_0}\left[ \boldsymbol{p}\cdot{\boldsymb...
...\left(\frac{1}{r^3}\right)+ \frac{1}{r^3}\nabla (\boldsymbol{p}\cdot r) \right]$](img67.png) |
||
![$\displaystyle =\frac{1}{4\pi\varepsilon_0}\left[ -\frac{\boldsymbol{p}}{r^3} +\frac{3\boldsymbol{r}\left(\boldsymbol{r}\cdot{\boldsymbol{p}}\right)}{r^5} \right]$](img69.png) |
(24) |
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年6月16日
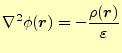
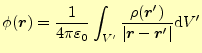
![\includegraphics[keepaspectratio, scale=1.0]{figure/electric_dipole.eps}](img47.png)