3 グリーンの定理
3.1 1変数関数の部分積分
グリーンの定理は,1変数の関数の部分積分の公式に似ている.部分積分は,関数の積の微分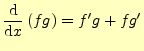 |
(19) |
から導ける.両辺を積分し,順番を入れ替えると
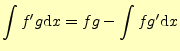 |
(20) |
となり,部分積分の公式が導かれた.
このように単純な方法で導かれる部分積分の公式は,本当に便利でいたるところに現れる. このベクトル解析版が,次に述べるグリーンの定理である.
3.2 スカラー場での部分積分
定理 3.1 (グリーンの定理)
スカラー場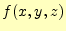 と
と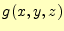 があるとする.この領域内の閉じた任意の部分を
があるとする.この領域内の閉じた任意の部分を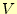 とする.そして,この
とする.そして,この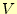 の境界面を
の境界面を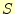 とする.すると,以下が成り立つ.
とする.すると,以下が成り立つ.
これをグリーンの定理という
スカラー場
これをグリーンの定理という
【証明】 1
ベクトル解析の恒等式
の両辺を体積積分する.左辺にはガウスの定理を用いると,
である.これで,式(21)が証明できた.
となる.同じように体積積分をしてガウスの定理を使うと,式(22)を得る ことができる.
の両辺を体積積分する.左辺にはガウスの定理を用いると,
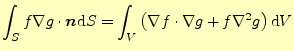 |
(24) |
である.これで,式(21)が証明できた.
式(23)と,これの![]() と
と![]() を入れ替変えたの辺々を引き
算すると,
を入れ替変えたの辺々を引き
算すると,
| (25) |
となる.同じように体積積分をしてガウスの定理を使うと,式(22)を得る ことができる.
注意 1
グリーンの定理は,
として,
と書かれる場合もある.
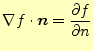 |
(26) |
として,
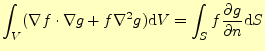 |
(27) |
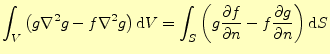 |
(28) |
と書かれる場合もある.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年5月26日
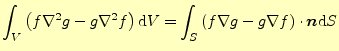
![\includegraphics[keepaspectratio, scale=1.0]{figure/green.eps}](img58.png)