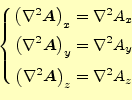8 ラプラス演算子

8.1 スカラーラプラス演算子

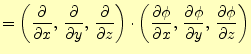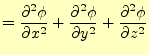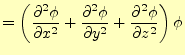式(36)の$\nabla^2$を考える．これは，

$$\nabla^2\phi =\nabla\cdot(\nabla \phi)$$

$$=\left( \if 11 \frac{\partial }{\partial x} \else \frac{\partial^... ...ial \phi}{\partial z} \else \frac{\partial^{1} \phi}{\partial z^{1}}\fi \right)$$

$$= \if 12 \frac{\partial \phi}{\partial x} \else \frac{\partial^{2... ...ac{\partial \phi}{\partial z} \else \frac{\partial^{2} \phi}{\partial z^{2}}\fi$$

$$=\left( \if 12 \frac{\partial \phi}{\partial x} \else \frac{\part... ...\phi}{\partial z} \else \frac{\partial^{2} \phi}{\partial z^{2}}\fi \right)\phi$$ (43)

となる．したがって，演算子$\nabla^2$は

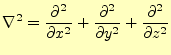$$\nabla^2= \if 12 \frac{\partial }{\partial x} \else \frac{\partia... ...f 12 \frac{\partial }{\partial z} \else \frac{\partial^{2} }{\partial z^{2}}\fi$$ (44)

である．この新しい演算子をラプラス演算子(ラプラシアン)と言う．$\nabla^2$の 代わりに$\Delta$と書くこともある．

これは，あたかもベクトル演算子同士の内積をとった結果，

$$\begin{aligned}\nabla\cdot\nabla &=\nabla^2\\ &=\left( \frac{\p... ...l^2}{\partial y^2}+ \frac{\partial^2}{\partial z^2} \end{aligned}$$

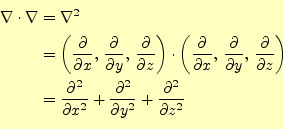のように見える．これが成り立つのは，カーテシアン座標系のみである．

これは，見て分かるようにスカラー演算子である．スカラー演算子であるため， スカラーやベクトルに作用することができる．スカラー場$\phi$に作用すると， 次のようなスカラー場ができる．

$$\begin{aligned}\nabla^2\phi &=\left( \frac{\partial^2}{\partial... ...\partial y^2}+ \frac{\partial^2 \phi}{\partial z^2} \end{aligned}$$

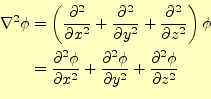このように単純に計算できるのはカーテシアン座標系の場合に限ら れる．ほかの曲線座標系のラプラス演算子は複雑である．円柱座標系と球座標系について は，詳細は，私のwebページに載せている．

http://www.akita-nct.jp/~yamamoto/study/electromagnetics/laplacian/html/index.html

を参考にせよ．

8.2 ベクトルラプラス演算子

ラプラス演算子がベクトル場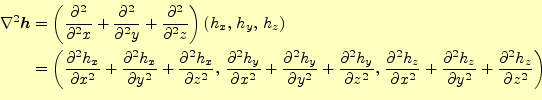 $\boldsymbol{h}$に作用すると，次のようなベクトル場ができる．

$$\begin{aligned}\nabla^2 \boldsymbol{h} &=\left( \frac{\partial^... ...l y^2}+ \frac{\partial^2 h_z}{\partial z^2} \right) \end{aligned}$$

カーテシアン座標系のみ，このような単純なことが言え，偶然の産物に過ぎない．実際に， ベクトル場に作用するベクトル演算子--ベクトルラプラシアン--は，ベクトル解析の恒等式

$$\nabla\times \nabla\times \boldsymbol{A}=\nabla \div{\boldsymbol{A}}-\nabla^2\boldsymbol{A}$$ (48)

から導くべきである．この式の右辺第2項がベクトルラプラス演算子(ベクトルラプラシアン)である． 従って，ベクトルラプラス演算子は，

$$\nabla^2\boldsymbol{A}=\nabla \div{\boldsymbol{A}}-\nabla\times \nabla\times \boldsymbol{A}$$ (49)

から計算できる．右辺は，勾配と発散，回転からなる．

カーテシアン座標系の $\textrm{x}$方向成分は，次のように地道に計算すれば求めることができる．

$$\left(\nabla^2\boldsymbol{A}\right)_x =(\nabla \div{\boldsymbol{A}})_x-(\nabla\times \nabla\times \boldsymbol{A})_x$$

$$=\left\{ \nabla\left( \frac{\partial A_x}{\partial x}+ \frac{\partial A_y}{\partial y}+ \frac{\partial A_z}{\partial z}\right) \right\}_x$$

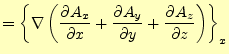$$\quad\qquad -\left\{\nabla\times\left[ \left( \if 11 \frac{\parti... ...ac{\partial^{1} A_x}{\partial y^{1}}\fi \right)\boldsymbol{k} \right]\right\}_x$$

$$= \if 11 \frac{\partial }{\partial x} \else \frac{\partial^{1} }{... ...rtial A_z}{\partial x} \else \frac{\partial^{1} A_z}{\partial x^{1}}\fi \right)$$

$$= \if 12 \frac{\partial A_x}{\partial x} \else \frac{\partial^{2}... ...frac{\partial A_x}{\partial z} \else \frac{\partial^{2} A_x}{\partial z^{2}}\fi$$

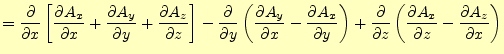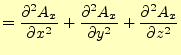$$=\nabla^2 A_x$$ (50)

カーテシアン座標形は，すべての軸が同じ形をしている．従って，他の軸のベクトルラプ ラス演算子は， $x \rightarrow y \rightarrow z$とサイクリックに記号を入れ替えるこ とにより容易に求められる．まとめると，カーテシアン座標系のベクトルラプラス演算子 は，

$$\left\{ \begin{aligned}\left(\nabla^2\boldsymbol{A}\right)_x &=... ...bla^2\boldsymbol{A}\right)_z &=\nabla^2 A_z \end{aligned} \right.$$

となる．実に，単純である．

ほかの曲線座標系のラプラス演算子は複雑である．円柱座標系と球座標系について は，詳細は，私のwebページに載せている．

http://www.akita-nct.jp/~yamamoto/study/electromagnetics/laplacian/html/index.html

を参考にせよ．
ホームページ: Yamamoto's laboratory
著者: 山本昌志