2 グリーン関数
2.1 ポアソン方程式とグリーン関数
数学的にグリーン関数をきっちり説明するとなると,厳密な定義と論理,計算が求められ厄介そ うである.また,直感的にイメージがつかみにくくなる.ここでは,こんなもんであると いうようなええかげんな話をする.数学的なちゃんとした定義を知りたければ,各自勉強せよ.図1のように,金属空洞の中に電荷が有る状況を考える.電荷は動か ないものとして,その中の静電ポテンシャルを求めよ--というのが問題である.当然こ れは,ポアソン方程式
を満足する.これを決められた境界条件--金属ではポテンシャルがゼロ--で計算すれば 良い.これは,今まで学習してきた通り.
つぎに,図2のような状況を考える.空洞中の場所
![]() にデルタ関数のような電荷が有る場合である.この場合,ポアソン方程
式は
にデルタ関数のような電荷が有る場合である.この場合,ポアソン方程
式は
となる.この
このグリーン関数が分かると,元のポアソン方程式(1)の解は,
と書くことができる.
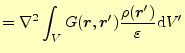 |
||
| |
||
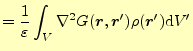 |
||
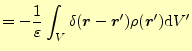 |
||
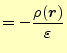 |
(4) |
式(3)は,ポアソン方程式の解になっているのである.
これの何がうれしいの?--と言う疑問があるだろう.これは,境界のみで決まる方程式
(2)の解
![]() が分かれば,内部にどの
ように電荷が分布
が分かれば,内部にどの
ように電荷が分布
![]() しようとも,積分を行うだけで,内部のポテンシャルが
分かると言っているのである.あとで分かるがかなり便利である.
しようとも,積分を行うだけで,内部のポテンシャルが
分かると言っているのである.あとで分かるがかなり便利である.
そもそもこのようなことが,言えるのはラプラス演算子が線形演算子になっているからで ある.式(4)までで,線形演算子といことを使っている.ど こだろうか?--捜してみよ.
2.2 もう少し一般的に
2.2.0.1 イメージ
なにも,グリーン関数はポアソン方程式に限らない.もう少しまともに,グリーン関数を 定義しよう.線形演算子を考える.
と書ける.このように解を書いたときに
となる.右辺は,
である.式(7)と式(8)の右 辺は,もともと式(6)の両辺から導いたものなので,等しい. すなわち,
![$\displaystyle -f(x)=\int \mathcal{L}\left[G(x,x^\prime)\right]f(x^\prime)\mathrm{d}x^\prime$](img26.png) |
(9) |
である.これから,
でなくてはならないことが分かる.これがグリーン関数を求めるときの微分方程式である. この微分方程式が成り立てば,式(6)は式 (5)の解となっている.
2.2.0.2 グリーン関数の検査
ある関数がグリーン関数になっているか否か?--調べたい.もちろん,微分方程式 (10)を満足していれば良い.左辺は微分なので計算でき る.したがって,最初の条件は| (11) |
となればよい.残りは,
が第二の条件となる.
本当は式(6)で定義されたグリーン関数が一意に決まることを 示さなくてはならないが,それは数学の教科書に任せる.それよりも,諸君はグリーン関 数の大まかな意味を知り,使いこなすことが重要である.
2.3 グリーン関数の例
いろいろな場面でグリーン関数は使われる.先に示したポアソン方程式を解くときのグリー ン関数は,| (13) |
である.他にもいろいろあるが,書いている時間が無い.自分で調べてみよ.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年9月24日
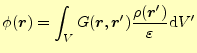
![\includegraphics[keepaspectratio, scale=1.0]{figure/poisson_eq.eps}](img17.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/green.eps}](img18.png)
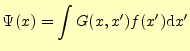
![$\displaystyle \mathcal{L}\int G(x,x^\prime)f(x^\prime)\mathrm{d}x^\prime= \int \mathcal{L}\left[G(x,x^\prime)\right]f(x^\prime)\mathrm{d}x^\prime$](img25.png)