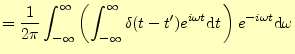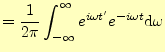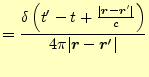3 ソースのある波動方程式の解
この辺の議論は,文献 [1]を参考にしている.というかほとん ど同じ.この教科書は上級者向きであるが分かりやすい.文献 [2]物理的なイメージを大事にして分かり易く説明している.以前の講義では,自由空間の波動方程式の解--ダランベールの解--を示した.それで, 分かったことは波が伝播することであった.この式だけでは,波の原因が分からない.一 般に,波の原因となるソース(源)を含んだ式は,
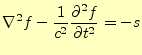 |
(14) |
のように記述される.この解をグリーン関数を使って,
計算する.式(10)より,グリーン関数が満たすべき微分 方程式は,
となる.この式のイメージを図3に示す.
これをいきなり解くのはのは大変である.時刻の微分がある場合の常套手段は,周波数領 域で計算することである.時刻を種は数に直すためにはフーリェ積分(変換)を使う.
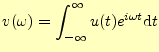 |
(17) | ||||
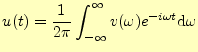 |
(18) |
時刻
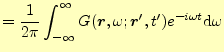 |
(19) |
となる.デルタ関数の方はちょっと面倒であるが,
のようにする.これはフーリェ級数を学習した時のおなじみの式である.これら,フーリェ積 分で表現されたグリーン関数とデルタ関数を元の式(16)に代 入すると
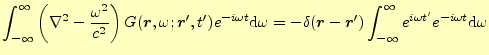 |
(21) |
が得られる.これが成り立つためには,
| (22) |
の条件が必要である.これを解き易くするために
| (23) |
と書き直す.つぎに,式(11)にしめしたようにグリーン関数は 同次微分方程式
| (24) |
を満たさなくてはならない.ここで,式を簡約するために,
| (25) |
となり,やっと解けるような気がする式になった.
対称性を考えると![]() は
は![]() を中心とした球対称な関数で,距離のみの関数はずである.そこで,
を中心とした球対称な関数で,距離のみの関数はずである.そこで,
![]() を
を![]() とおいて,球座標系のラプラシアンを導入すると
とおいて,球座標系のラプラシアンを導入すると
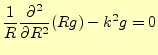 |
(26) |
となる.この微分方程式の一般解は,
| (27) |
となる.したがって,
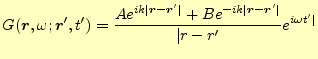 |
(28) |
となる.積分定数の
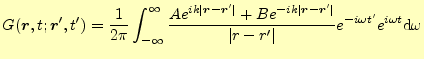 |
(29) |
ここで,係数
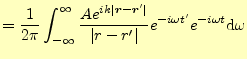 |
||
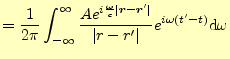 |
(30) |
となる.式(20)の示すところによると,この式の右辺は
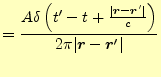 |
(31) |
となる.積分定数
となる.
計算は結構複雑で,わかり難かったと思う.私もわかり難い.straght fowardの計算となっ ていない.もう少し簡単な方法を考えなくてはならない.計算過程は複雑であったが,そ の結果は直感的に分かる.直感的に導くこともできるであろう.この式の言っていること は,次のとおりである.
- 波の振幅は,距離に反比例する.よく知られているように波のエネルギーは振幅 の2乗に比例する.そして3次元の波は距離2乗に比例して表面積が大きくなる.したがっ て,エネルギーが保存するためには波の振幅は距離に比例しなくてはならない.当たり 前の結果が得られている.
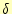 関数の部分が言っていることは,波の速度は
関数の部分が言っていることは,波の速度は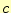 で伝わる--ということで
ある.観測点で波を観測する時刻
で伝わる--ということで
ある.観測点で波を観測する時刻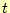 を求めてみよ(
を求めてみよ(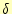 関数の独立変数がゼロとな
るとき).
関数の独立変数がゼロとな
るとき).
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年9月24日
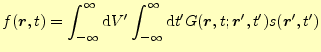
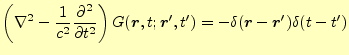
![\includegraphics[keepaspectratio, scale=0.7]{figure/wave_source_green_fun.eps}](img39.png)