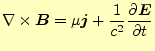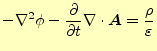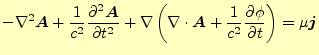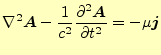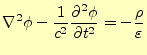4 電磁ポテンシャル
実際にマクスウェルの方程式を解くとなるとかなりやっかいである.電場と磁場,そして ソース(源)としての電荷や電流が入り乱れている.そこで,電磁ポテンシャルというもの が導入すれば,見通しの良い式に直すことができる.ただ,見通しの善し悪しは解くべき 問題にかなり依存する.先の電場4.1 静電磁場のポテンシャル
静電場の学習で,スカラーポテンシャル| (23) |
である.これは,静電場の
| (24) |
というようなベクトル場
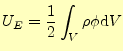 |
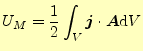 |
(25) |
となる.
ところで,式(21)の
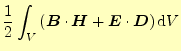 |
(26) |
も電磁場のエネルギーを表している.これと,ポテンシャルを使ったエネルギーはどのよ うに違うのだろうか?.考え方は異なるが,まったく同じ物理的な内容である.かたや場 のエネルギーという考え方,もう一方は電荷や電流がポテンシャルエネルギーと持つと考 えている.いずれの場合でも計算結果は同じである.
4.2 時間変動する場への拡張
静電場や静磁場のスカラーポテンシャルとベクトルポテンシャルは,先の説明で終わり である.ポテンシャルの考え方は何かと便利なので,時間的に変動する電磁場にも導入し たい.そこで,静電磁場のポテンシャルを拡張することを考える.ベクトルポテンシャル は,静磁場の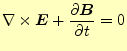 |
(27) |
と左辺を移項して
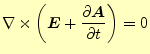 |
(28) |
と書き換える.すると,回転がゼロとなるべくとる場は,あるスカラー場の勾配と書くこ とができる.あるスカラー場を
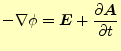 |
(29) |
である.マイナスがつくのは習慣に過ぎない.したがって,電場は
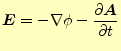 |
(30) |
と表すことができる.
これらのスカラーポテンシャル![]() とベクトルポテンシャル
とベクトルポテンシャル
![]() を導入することで,
マクスウェルの方程式を書き換える.
を導入することで,
マクスウェルの方程式を書き換える.
![]() と
と
![]() をつかい,さらに
をつかい,さらに
![]() とすると,マクスウェルの方程式は
とすると,マクスウェルの方程式は
となる.これらの連立微分方程式は,元の方程式(1)-(4)と同じくらい複雑である.10個の式に10個の未知数が含まれる連 立微分方程式となっている.こんなに複雑だとポテンシャルを導入したメリットはない. そこで,これらの式を変形して,変数分離形にすることを目指す.具体的には,ベクトル ポテンシャルとスカラーポテンシャルのそれぞれの微分方程式を導くのである.
まずは,式(33)をベクトルポテンシャルとスカラーポテンシャル で書き換える.式(33)に式(32)を代入すると
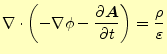 |
(35) |
となり,整理すると
である.
つぎに,式(34)に式(33)に 式(32)を代入する.すると,
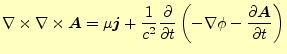 |
(37) |
となる.これをベクトル恒等式
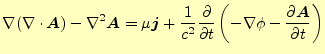 |
(38) |
のように書き直す.整理すると
となる.
これで,マクスウェルの方程式は,式(36)と(39) で表せたことになる.これでもまだ複雑で実際の計算に使う気にはなれない.もう少し簡 単にできる.ベクトル場は,回転と発散により決めることができる--ということを使う. ベクトルポテンシャルの回転は,式(31)により決められている. 発散の方は特に制限がなく,勝手に決めることができる.そこで,
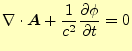 |
(40) |
のように決める.これをローレンツゲージと言う.本当はこの辺は,もっと詳しく説明す る必要があるが,かんべんしてほしい.取り合えずこのようにするのである.すると,
となる.2つとも波動方程式で,ベクトルポテンシャルの源は電流で,スカラーポテンシャ ルの源は電荷となっている.それにしても,対称性がよく美しい式である.
マクスウェルの方程式(1)-(4)の代わりに, これらの波動方程式(41)と(42)を解けばよいのであ る.大幅に式は簡単になった.そして対称性も良いので計算が楽になることは明らかであ る.本講義の最後の章「電磁波の放射」でこの式の威力が分かるだろう.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年7月13日