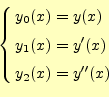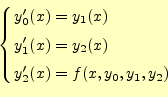2 常微分方程式
数値計算により,近似解を求める微分方程式は,である.これは問題として与えられ,この式に従う
2.1 4次のルンゲ・クッタ法
前期末試験で出題したオイラー法や2次のルンゲ・クッタ法は,パラメーターを増やして 誤差項の次数を上げていく方法である.この方法で最良と言われるのが4次のルンゲ・クッ タ法である.パラメーターを増やして,5, 6, 7,ということで,皆さんが常微分方程式を計算する必要が生じたときは,何はともあれ4次 のルンゲ・クッタで計算すべきである.普通の科学に携わる人にとって,4次のルンゲ・ クッタは常微分方程式の最初で最後の解法である.
4次のルンゲ・クッタの公式は,式(2)に示す通りである.そし て,これは図1のように表すことができる.
2.2 プログラム(4次のルンゲ・クッタ法)
実際の微分方程式を4次のルンゲ・クッタ法で計算するプログラムを示す.計算結果は,配列「x[]」と 「y[]」に格納される.実際にプログラムでは,この結果を利用してグラフにしたりする のであるが,ここでは計算のみとする.
#include <stdio.h>
#include <math.h>
#define IMAX 100001
double func(double x, double y);
/*================================================================*/
/* main function */
/*================================================================*/
int main(void){
double x[IMAX], y[IMAX];
double final_x, h;
double k1, k2, k3, k4;
int ncal, i;
/*--- set initial condition and cal range ---*/
x[0]=0.0;
y[0]=0.0;
final_x=10.0;
ncal=10000;
/* --- size of calculation step --- */
h=(final_x-x[0])/ncal;
/* --- 4th Runge Kutta Calculation --- */
for(i=0; i < ncal; i++){
k1=h*func(x[i],y[i]);
k2=h*func(x[i]+h/2.0, y[i]+k1/2.0);
k3=h*func(x[i]+h/2.0, y[i]+k2/2.0);
k4=h*func(x[i]+h, y[i]+k3);
x[i+1]=x[i]+h;
y[i+1]=y[i]+1.0/6.0*(k1+2.0*k2+2.0*k3+k4);
}
return 0;
}
/*================================================================*/
/* define function */
/*================================================================*/
double func(double x, double y){
double dydx;
dydx=sin(x)*cos(x)-y*cos(x);
return(dydx);
}
2.3 高階の常微分方程式
2.3.1 1階の連立微分方程式に変換
ここまで示した方法は,1階の常微分方程式しか取り扱えないので不便である.そこで, 高階の常微分方程式を1階の連立微分方程式に直す方法を示す.要するに,高階の常微分 方程式を連立1階常微分方程式に直し,4次のルンゲ・クッタ法を適用すれば良いのである. 例えば,次のような3次の常微分方程式があったする.この3階常微分方程式を次に示す式を用いて変換する.
この式を用いて,式(4)を書き直すと
となる.これで,3階の常微分方程式が3元の1階の連立常微分方程式に変換できた.2階で あろうが4階
2.3.2 練習問題
以下の高次常微分方程式を連立1階微分方程式に書き換えなさい.ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年11月27日
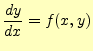
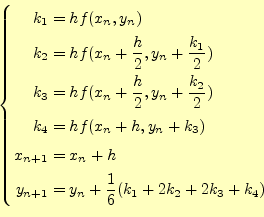
![\includegraphics[keepaspectratio, scale=0.7]{figure/diff_eq/RK4.eps}](img13.png)