1 常微分方程式
1.1 常微分方程式のイメージ
微分方程式は,物理や工学の分野で問題を解く強力なツールばかりか,生物や経済などで も広く応用されている.自然科学や工学の問題を定量的に考察する場合,微分方程式ほど 強力な道具はない.この微分方程式を使うためには,方程式をる作ことと解くことが必要 である.ここでは,微分方程式を解くこと,特に数値計算により非常に精度の良い近似値 を求める方法を学習する.微分方程式には解析解が無いのが普通であるが,理工学上の諸 問題では精度良く解の近似値を求めたい状況にしばしば遭遇する.このような時,数値計 算の出番となる.数学に無い面白さがありますので,楽しんでください.すでに学習したように,独立変数が二つ以上の多変数の関数の微分(偏微分)を含む微分方 程式を偏微分方程式(partial differential equation)という.それに対して,一変数の 関数の微分を含む方程式を常微分方程式(ordinary differential equation)という.ここ では,常微分方程式,特に1 階の場合の解の近似値を求める方法を学習する.学習する方 程式の形は
である.1階だといってバカにはできない.後で述べることになるが,これが数値計算 できると,どんな高階の常微分方程式も同じ方法で計算ができるのである.数学だと1 解 が解ければ高階の微分方程式が解けるわけではないが,数値計算では可能なのである.
ここでの主題は,この微分方程式を満たす![]() を求めることになる.計算を進める前に,
この方程式が何を表すか考えることにする.式(1) の左辺は,解
を求めることになる.計算を進める前に,
この方程式が何を表すか考えることにする.式(1) の左辺は,解
![]() の導関数となっている.即ち,解の曲線の接線を表す.導関数の値が座標
の導関数となっている.即ち,解の曲線の接線を表す.導関数の値が座標![]() の関数になっているので,座標が決まれば,その場の曲線の傾きが決きまることになる.
の関数になっているので,座標が決まれば,その場の曲線の傾きが決きまることになる.
それでは,この常微分微分方程式のイメージをつかむことにする.それには,実際 の微分方程式を考えるのが良いであろう.例えば,
のような常微分方程式を考えることにする.いかにも難しげな微分方程式であるが,これ には解析解がある.解析解はとりあえずおいておくことにして,この式の右辺を考える. 先ほど述べたように,これは接線の傾きを表す.場所ごとに接線の傾きが決まっているの で,それを
この微分方程式の解析解は,
| (3) |
である.1階の微分方程式なので,1個の未知数を含む.この未知数の値が異なる5本の曲 線と,先ほどの方向場を重ねて書きすると,図2のようになる.微分方 程式の解である曲線
式(2)の微分方程式から,関数![]() の値を得るにはもう一つ条件が必
要である.通常この条件は,
の値を得るにはもう一つ条件が必
要である.通常この条件は,
![]() のように与えられる.これを初期値といい,初
期値が与えられるものを初期値問題という.一方,2 点以上のxで定めるyの値が決まって
いるような問題を境界値問題という2.ここでは,もっぱら初期値問題
を解くことにする.
のように与えられる.これを初期値といい,初
期値が与えられるものを初期値問題という.一方,2 点以上のxで定めるyの値が決まって
いるような問題を境界値問題という2.ここでは,もっぱら初期値問題
を解くことにする.
1.2 数値計算のイメージ
初期値問題を計算するルーチンの基礎的な考え方はどれも似通っており,次に述べるとお りである.まず,(1)式の微分方程式を極限の| (4) |
のように近似できる.これを用いて,
この式と初期値
式(5)は,
- 次の
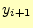 値は,もとの
値は,もとの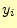 に,そこでの傾き
に,そこでの傾き
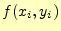 に
に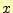 の増分
の増分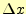 を乗じたものを加えることにより求められる.
を乗じたものを加えることにより求められる.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年9月5日
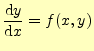
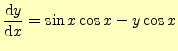
![\includegraphics[keepaspectratio, scale=1.0]{figure/direction_field.eps}](img14.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/solution.eps}](img16.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/sabun.eps}](img32.png)