3 フーリエ積分・変換
3.1 フーリエ級数
次のような関数はフーリエ級数で表すことができる. -4pt- 周期的に繰り返す関数
- 有限な区間で定義された関数
![$\displaystyle =\frac{a_0}{2} +\sum_{n=1}^{\infty}\left[ a_n\cos \frac{n\pi x}{L} +b_n\sin \frac{n\pi x}{L} \right]$](img28.png) |
(4) | |
ただし,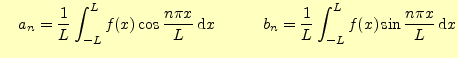 |
のようにフーリエ級数で表すことができる.
3.2 フーリエ積分
先に示したように,フーリエ級数は有限な区間が得られる.ここで,
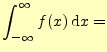 有限の値 有限の値 |
(6) |
とするならば,式(5)の右辺の第一項はゼロに収束する4.なぜならば,
| (7) | ||
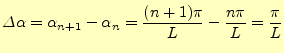 |
(8) |
とおく.すると,
となる.ここで,
とおく.すると,式(9)は,
となる.この右辺はリーマン和の極限--普通の積分--の形になっている.したがって,
と書くことができる.これまでの話をまとめると,次のようになる.
フーリエ積分1
区間
|
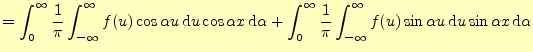 |
||
![$\displaystyle =\frac{1}{\pi}\int_0^{\infty}\int_{-\infty}^{\infty} f(u)\left[ \...
... u\cos\alpha x+\sin\alpha u\sin\alpha x \right] \,\mathrm{d}u\,\mathrm{d}\alpha$](img62.png) |
||
|
三角関数の加法定理を使うと
| ||
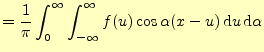 |
(14) | |
がえられる.これもフーリエ積分である.
3.3 フーリエ積分(指数関数形)
式(14)から,指数関数を用いたフーリエ積分を求める.その 計算をするときに,オイラーの公式より導くことができる.ここでは,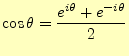 |
(15) |
を用いる.
この式を使うと,式(14)は次のように変形できる.
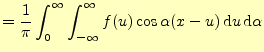 |
||
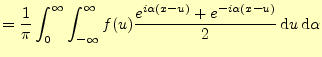 |
||
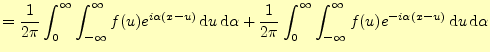 |
||
|
右辺第二項を
| ||
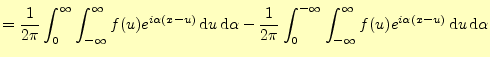 |
||
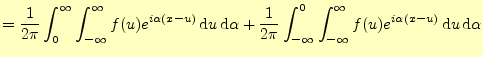 |
||
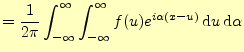 |
(16) | |
この式は,一般には次のように変形されて使われることが多い.
この式もまた,フーリエ積分の別の形である.他のフーリエ積分に比べると式が単純であ ること,また次のフーリエ変換との関係が深いことから,これがもっとも重要である.
3.4 フーリエ変換
式17から,次のような関係式を導くことができる 5.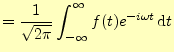 |
(18) | |
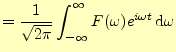 |
(19) |
これをフーリエ変換(Fourier transform)と言う.これは,時間情報を周波数情報に変換 している.すなわち,時刻の関数で振幅が
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年2月28日
![$\displaystyle f(x)=\frac{1}{2L}\int_{-L}^{L}f(x)\,\mathrm{d}x+\frac{1}{L}\sum_{...
...sin \frac{n\pi x}{L}\int_{-L}^{L}f(u)\sin \frac{n\pi u}{L}\,\mathrm{d}u \right]$](img37.png)
![$\displaystyle f(x)=\lim_{\varDelta\alpha\to 0} \frac{\varDelta\alpha}{\pi}\sum_...
...in(\alpha_n x)\int_{-\infty}^{\infty} f(u)\sin(\alpha_n u)\,\mathrm{d}u \right]$](img46.png)
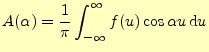
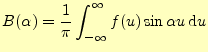
![$\displaystyle =\lim_{\varDelta\alpha\to 0}\varDelta\alpha\sum_{n=1}^{\infty}\left[ \cos(\alpha_n x)A(\alpha_n) +\sin(\alpha_n x)B(\alpha_n) \right]$](img50.png)
![$\displaystyle =\lim_{\varDelta\alpha\to 0}\sum_{n=1}^{\infty}\left[ \cos(\alpha...
...)A(\alpha_n)\varDelta\alpha +\sin(\alpha_n x)B(\alpha_n)\varDelta\alpha \right]$](img51.png)
![$\displaystyle =\lim_{\varDelta\alpha\to 0}\left[\sum_{n=1}^{\infty} A(\alpha_n)...
...a\alpha +\sum_{n=1}^{\infty} B(\alpha_n)\sin(\alpha_n x)\varDelta\alpha \right]$](img52.png)
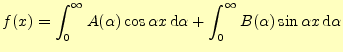
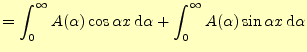
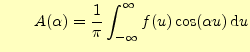
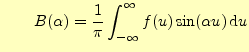
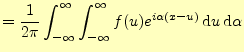
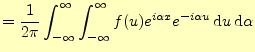
![$\displaystyle =\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\left[ \frac{1}{\sqr...
...{\infty} f(u)e^{-i\alpha u}\,\mathrm{d}u \right]e^{i\alpha x}\,\mathrm{d}\alpha$](img78.png)