2 パーセバルの等式
これまで学習したように,区間![$\displaystyle =\frac{a_0}{2} +\sum_{n=1}^{\infty}\left[ a_n\cos \frac{n\pi x}{L} +b_n\sin \frac{n\pi x}{L} \right]$](img14.png) |
(1) | |
ただし,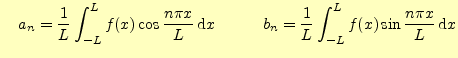 |
のようにフーリエ級数で表すことができる.式(4)の両辺に
![$\displaystyle \int_{-L}^{L}\left[f(x)\right]^2\,\mathrm{d}x$](img17.png) |
![$\displaystyle =\int_{-L}^{L}\frac{a_0}{2}f(x)\,\mathrm{d}x +\int_{-L}^{L}\sum_{...
...eft[ a_n\cos \frac{n\pi x}{L}+b_n\sin \frac{n\pi x}{L} \right]f(x)\,\mathrm{d}x$](img18.png) |
|
![$\displaystyle =\frac{a_0}{2}\int_{-L}^{L}f(x)\,\mathrm{d}x +\sum_{n=1}^{\infty}...
...L}\,\mathrm{d}x +b_n\int_{-L}^{L}f(x)\sin \frac{n\pi x}{L}\,\mathrm{d}x \right]$](img19.png) |
||
| 式(4)の |
||
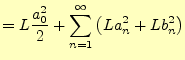 |
(2) |
以上より,
が得られる.これをパーセバルの等式と言う.直交関数系のピタゴラスの定理のよ うなものである.フーリエ級数の収束の確認に有効である.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年2月28日
![$\displaystyle =\frac{a_0}{2} +\sum_{n=1}^{\infty}\left[ a_n\cos \frac{n\pi x}{L} +b_n\sin \frac{n\pi x}{L} \right]$](img14.png) |
(1) | |
ただし,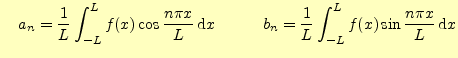 |
![$\displaystyle \int_{-L}^{L}\left[f(x)\right]^2\,\mathrm{d}x$](img17.png) |
![$\displaystyle =\int_{-L}^{L}\frac{a_0}{2}f(x)\,\mathrm{d}x +\int_{-L}^{L}\sum_{...
...eft[ a_n\cos \frac{n\pi x}{L}+b_n\sin \frac{n\pi x}{L} \right]f(x)\,\mathrm{d}x$](img18.png) |
|
![$\displaystyle =\frac{a_0}{2}\int_{-L}^{L}f(x)\,\mathrm{d}x +\sum_{n=1}^{\infty}...
...L}\,\mathrm{d}x +b_n\int_{-L}^{L}f(x)\sin \frac{n\pi x}{L}\,\mathrm{d}x \right]$](img19.png) |
||
| 式(4)の |
||
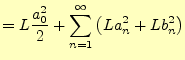 |
(2) |