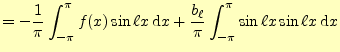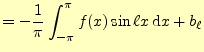2 最良近似としてのフーリエ級数
2.1 最小二乗法
最小二乗法というのは,データをある関数で最良近似する方法である.例えば,| (1) |
の
となる.
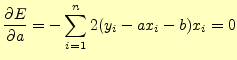 |
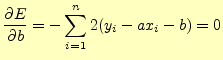 |
(3) |
これは,
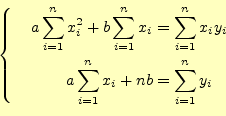 |
である.これを解くと
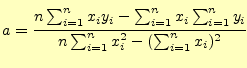 |
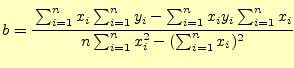 |
(5) |
となる.
最初に示したのデータについて計算してみると,
![]() となる.ゆ
えに,最小二乗法による1次関数は
となる.ゆ
えに,最小二乗法による1次関数は
| (6) |
となる.データをこの間数をプロットすると,図1のようになる.
グラフ作成ソフトウェアーは,最小二乗法によるデータのフィッティングをサポートして いるものが多い.EXCELでも可能なはずである.実験データの整理に使うと良い.
ここでは,偏微分により最小二乗法の式を導いたが,線形代数の部分空間への射影を考え る方が簡単である.これについては,参考文献 [2]に詳しく書い てある.これは良い教科書なので,一読を勧める.
2.2 フーリエ級数の最小二乗法
2.2.1 誤差の積分
ここでは,フーリエ級数で関数をフィッティングした場合の誤差を考える.
区間
![]() で定義された関数
で定義された関数![]() は,
は,
のようにフーリエ級数で表すことができる.例えば,
と表すことができる.ここで,区間
![$\displaystyle E=\frac{1}{2\pi}\int_{-\pi}^\pi\left\{x-2\left[\sin x-\frac{\sin ...
... 3x}{3}- \dots+(-1)^{n+1}\frac{\sin nx}{n}+\cdots\right]\right\}^2\,\mathrm{d}x$](img38.png) |
(9) |
積分の前に
2.2.2 三角関数でフィットするときの最小二乗法
フーリエ級数とは全く話を別にして,区間で近似する.なんか,フーリエ級数そっくりではないか?--とツッコミをいれたくなるが, それとはまったく別なもの,フーリエ級数など知らないとして,話を進める.ある関数
と定義する.この二乗平均誤差は,係数
誤差を表す式(11)を最小にするには,![]() と
と![]() をどのように選ぶか?--
ということが問題となる.これを最小にするということは,関数
をどのように選ぶか?--
ということが問題となる.これを最小にするということは,関数![]() を三角関数で近似
する最適な係数を決めることに他ならない.式(11)には最小値があり,関
数を近似する最適な
を三角関数で近似
する最適な係数を決めることに他ならない.式(11)には最小値があり,関
数を近似する最適な![]() と
と![]() がある.なぜならば,全ての
がある.なぜならば,全ての![]() と
と![]() は係数が正の
2次式であるため,最小値があるからである.この最小値はそれぞれの偏微分がゼロに
なるときに得られる.すなわち,
は係数が正の
2次式であるため,最小値があるからである.この最小値はそれぞれの偏微分がゼロに
なるときに得られる.すなわち,
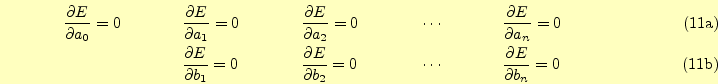 |
が条件となる.この具体的な計算は,式(11)に式(10)を代入 して偏微分がゼロとなる
2.2.2.1 準備
これらの式は,第4回の講義で話した内容である.
2.2.2.2 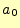 の計算
の計算
二乗平均後差が最小になる| 0 | 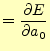 |
|
![$\displaystyle =-\frac{1}{2\pi}\int_{-\pi}^{\pi}2\left\{ f(x)-\left[\frac{a_0}{2}+\sum_{k=1}^n(a_k\cos kx+b_k\sin kx)\right] \right\}\frac{1}{2}\,\mathrm{d}x$](img74.png) |
||
|
式(15)より
| ||
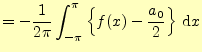 |
||
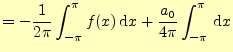 |
||
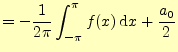 |
(16) | |
である.ゆえに,
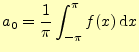 |
(17) |
となる.これは,フーリエ級数の
2.2.2.3 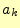 の計算
の計算
二乗平均後差が最小になるしたがって,
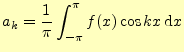 |
(19) |
である.これもフーリエ係数の計算と同じ
2.2.2.4 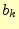 の計算
の計算
同様にし,二乗平均後差が最小になるしたがって,
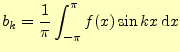 |
(21) |
である.これもフーリエ係数の計算と同じ.
2.2.3 まとめ
フーリエ級数は,関数ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年12月1日
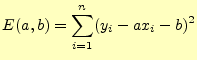
![\includegraphics[keepaspectratio, scale=1.0]{figure/lsm.eps}](img26.png)
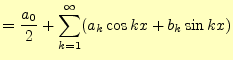
![$\displaystyle f(x)=2\left[\sin x-\frac{\sin 2x}{2}+\frac{\sin 3x}{3}- \dots+(-1)^{n+1}\frac{\sin nx}{n}+\cdots\right]$](img34.png)
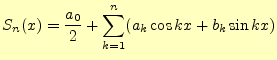
![$\displaystyle E(a_0,\,a_1,\,a_2,\,\cdots,\,a_n;\,b_1,\,b_2,\,\cdots,\,b_n)= \frac{1}{2\pi}\int_{-\pi}^{\pi}[f(x)-S_n(x)]^2\,\mathrm{d}x$](img53.png)
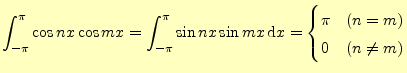
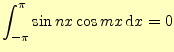
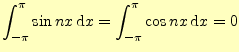
![$\displaystyle =-\frac{1}{2\pi}\int_{-\pi}^{\pi}2\left\{ f(x)-\left[\frac{a_0}{2}+\sum_{k=1}^n(a_k\cos kx+b_k\sin kx)\right] \right\}\cos \ell x\,\mathrm{d}x$](img86.png)
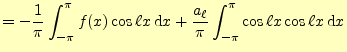
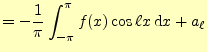
![$\displaystyle =-\frac{1}{2\pi}\int_{-\pi}^{\pi}2\left\{ f(x)-\left[\frac{a_0}{2}+\sum_{k=1}^n(a_k\cos kx+b_k\sin kx)\right] \right\}\sin\ell x\,\mathrm{d}x$](img94.png)