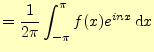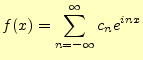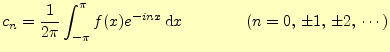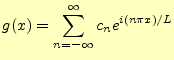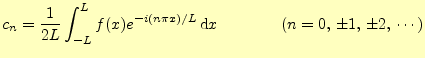3 複素フーリエ級数
三角関数の計算は厄介なので,指数関数を使った方が便利なことが多い.そこで,複素数 の指数関数を使ったフーリエ級数を考える.そのためには,2回目の講義で述べたオイラー の公式が重要な役割を果たす.これから
を直ちに導くことができる.これを,フーリエ級数の式(7)に代 入すると,
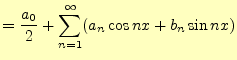 |
||
![$\displaystyle =\frac{a_0}{2}+\sum_{n=1}^\infty\left[ a_n\frac{e^{inx}+e^{-inx}}{2}+b_n \frac{e^{inx}-e^{-inx}}{2i}\right]$](img104.png) |
||
![$\displaystyle =\frac{a_0}{2}+\sum_{n=1}^\infty\left[ \frac{a_n}{2}(e^{inx}+e^{-inx})-\frac{ib_n}{2}(e^{inx}-e^{-inx})\right]$](img105.png) |
||
![$\displaystyle =\frac{a_0}{2}+\sum_{n=1}^\infty\left[ \frac{1}{2}(a_n-ib_n)e^{inx}+\frac{1}{2}(a_n+ib_n)e^{-inx}\right]$](img106.png) |
となる.これは,いままでと同一の式である.左辺は実数で,右辺の値も実数となる.右辺に は虚数部が含まれるが,それはキャンセルされてゼロとなる.ここで,
| (24) |
とする4.すると,かなり形式的ではあるが,
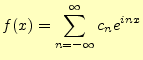 |
(25) |
が得られる.これを複素フーリエ級数という.フーリエ係数
よく見ると,係数を計算する3つの式(27)(28)(29)は,
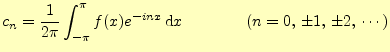 |
(29) |
とまとめることができる.
そして,![]() と
と![]() は複素共役の関係
は複素共役の関係
| (30) |
がある.
区間![]() で定義された関数
で定義された関数![]() の場合,ほとんど同じ議論で,
の場合,ほとんど同じ議論で,
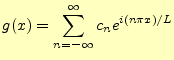 |
(31) |
となる.係数は,
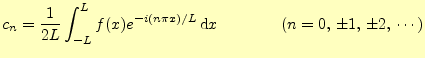 |
(32) |
と導くことができる.
まとめ(複素フーリエ級数)
|
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年12月1日
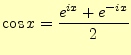
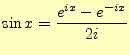
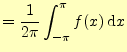
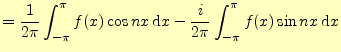
![$\displaystyle =\frac{1}{2\pi}\int_{-\pi}^\pi f(x)[\cos nx-i\sin nx] \,\mathrm{d}x$](img122.png)
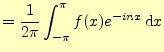
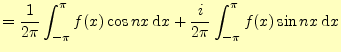
![$\displaystyle =\frac{1}{2\pi}\int_{-\pi}^\pi f(x)[\cos nx+i\sin nx] \,\mathrm{d}x$](img128.png)