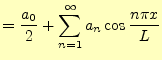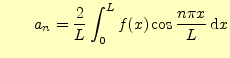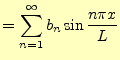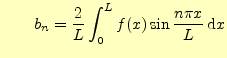3 フーリエ余弦級数とフーリエ正弦級数
3.1 偶関数と奇関数
関数の対称性を考えると,フーリエ係数を求める積分が容易になることがある.ここでは, 関数の対称性として,偶関数と奇関数を考える.
![]() ならば偶関数(even function),
ならば偶関数(even function),
![]() ならば奇関数(odd function)
であるという.図3や4に示すように,偶
関数はy軸について対称,奇関数は原点について対称になる.諸君が知っている関数では,
次のようなものがある.
ならば奇関数(odd function)
であるという.図3や4に示すように,偶
関数はy軸について対称,奇関数は原点について対称になる.諸君が知っている関数では,
次のようなものがある.
偶関数の例偶関数,奇関数の名前の由来???.
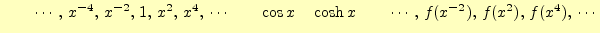
奇関数の例
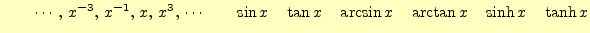
どちらでもない
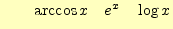
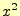 の場合,
の場合,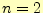 は偶数;偶関数となる.
は偶数;偶関数となる.
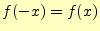 の関係がありy軸
に対称である.
の関係がありy軸
に対称である.
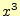 の場合,
の場合,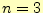 は奇数;奇関数となる.
は奇数;奇関数となる.
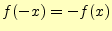 の関係があり原点
に対称である.
の関係があり原点
に対称である.
関数同志の演算に関して,次のような関係がある.偶関数であれば
![]() ,奇関数
であれば
,奇関数
であれば
![]() から,これは容易に理解できる.
から,これは容易に理解できる.
| 偶 |
偶 |
偶 |
偶 |
||||||
| 奇 |
奇 |
奇 |
奇 |
||||||
| 偶 |
偶 |
偶 |
偶 |
さらに,対称性より次の積分の関係も得られる.積分は
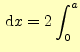 偶関数 偶関数 |
(6) |
3.2 偶関数と奇関数のフーリエ級数
偶関数あるいは奇関数の周期関数は,しばしば出会う.このような場合,フーリエ級数は 少しだけ簡単になる.
周期![]() の関数
の関数![]() のフーリエ級数は式(5)から計算するこ
とができる.ここで,
のフーリエ級数は式(5)から計算するこ
とができる.ここで,![]() が偶関数あるいは奇関数の場合を考える.フーリエ係数
が偶関数あるいは奇関数の場合を考える.フーリエ係数
![]() と
と![]() は,つぎの積分より求めることができる.
は,つぎの積分より求めることができる.
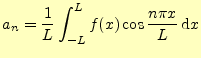 |
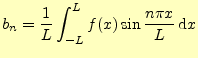 |
(7) |
もし,
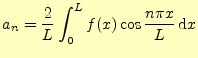 |
(8) |
となる.なぜならば,被積分関数
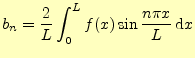 |
(9) |
となる.これらをまとめると,次の結果が得られる.
フーリエ余弦級数と正弦級数
|
ここで,ちょっと余談であるが,面白いことを述べよう.対称性の無い関数![]() は,式
(5)のようにフーリエ級数で表すことができる.この式の右
辺は,偶関数であるフーリエ余弦級数と奇関数であるフーリエ正弦級数の和になっている.
このことは,対称性のない周期関数であろうとも,偶関数と奇関数に分解できることを示
している.すなわち,
は,式
(5)のようにフーリエ級数で表すことができる.この式の右
辺は,偶関数であるフーリエ余弦級数と奇関数であるフーリエ正弦級数の和になっている.
このことは,対称性のない周期関数であろうとも,偶関数と奇関数に分解できることを示
している.すなわち,
| 任意の周期関数 |
(12) |
である.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年11月7日
![\includegraphics[keepaspectratio, scale=1.0]{figure/even_function.eps}](img80.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/odd_function.eps}](img81.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/non_sym_function.eps}](img82.png)