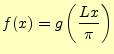2 周期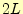 の周期関数のフーリエ級数
の周期関数のフーリエ級数
前回,周期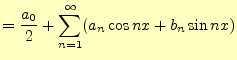 |
(1) | |
ただし,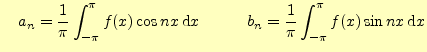 |
とフーリエ級数で表せる.これを,任意の周期
図1のような周期![]() の関数
の関数![]() を考える.この関数の横軸
を
を考える.この関数の横軸
を![]() 倍すると,図2のような周期
倍すると,図2のような周期![]() の関数
の関数![]() ができあがる.したがって,この
ができあがる.したがって,この![]() は式(1)のようにフー
リェ級数で表すことができる.
は式(1)のようにフー
リェ級数で表すことができる.
ところで,関数の横軸を![]() 倍するということはどういうことであろうか?.図から
も分かるように,次の関係
倍するということはどういうことであろうか?.図から
も分かるように,次の関係
が成り立つことに他ならない.直感的に理解できない--というならば,
ここで,![]() は
は![]() の周期関数なので,式(1)のようにフー
リエ級数で表すことができる.一方で,関数
の周期関数なので,式(1)のようにフー
リエ級数で表すことができる.一方で,関数![]() と
と![]() は式(2)の関
係がある.ゆえに,
は式(2)の関
係がある.ゆえに,
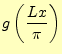 |
(3) | |
ただし,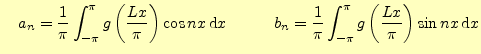 |
となる.ここで,
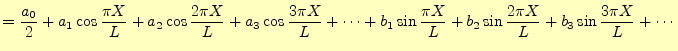 |
(4) | |
ただし,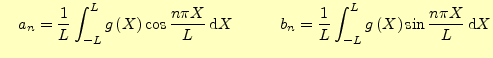 |
が得られる.これを,形式的に
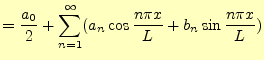 |
(5) | |
ただし,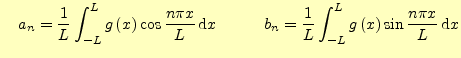 |
となる.これが,任意の周期
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年11月7日
![\includegraphics[keepaspectratio, scale=0.8]{figure/periodic_func_2L.eps}](img36.png)
![\includegraphics[keepaspectratio, scale=0.8]{figure/periodic_func_2pi.eps}](img45.png)