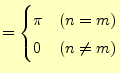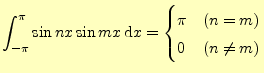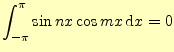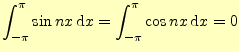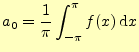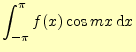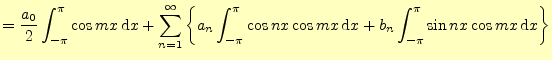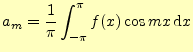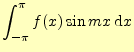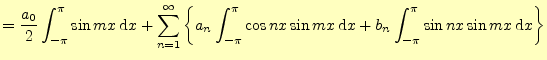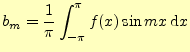2 フーリェ級数
2.1 三角関数を用いた展開
前々回の講義で,任意の関数を冪級数で展開(テイラー展開)した.ここでは,もっとけっ たいなことを考えて三角関数で展開してみよう.すなわち,と展開する.最初の項は
この展開式を見て諸君は,展開の係数![]() と
と![]() をもとめることに興味があるだろう.そ
れをぐっと我慢して,まず関数
をもとめることに興味があるだろう.そ
れをぐっと我慢して,まず関数![]() の右辺の性質を考えることにしよう.関数
の右辺の性質を考えることにしよう.関数![]() は,
は,![]() の周期性という重要な性質がある.定数項である
の周期性という重要な性質がある.定数項である![]() は,
は,
![]() としても値は変わらいない.三角関数の項も,
としても値は変わらいない.三角関数の項も,
![]() としても値は変わらない.なぜならば,
としても値は変わらない.なぜならば,
| (2) |
となるからである.すなわち式(1)は,
| (3) |
となっている.式(1)のどんな
| (4) |
が得られる.明らかに
式(1)の![]() は,
は,![]() を周期とした任意の関数である.任意
の周期関数は,三角関数の和で表すことができる--と言っている.このように周期関数
を三角関数の和で表すことを,フーリェ級数3(Fourier series)と言う.別の考え方
をすると,区間の幅が
を周期とした任意の関数である.任意
の周期関数は,三角関数の和で表すことができる--と言っている.このように周期関数
を三角関数の和で表すことを,フーリェ級数3(Fourier series)と言う.別の考え方
をすると,区間の幅が![]() ,例えば
,例えば
![]() のどんな関数でも三角関数の和で表す
ことができると式(1)は言っている.テイラー展開は任意の関数
を冪乗の和で表したが,フーリェ級数は三角関数の和で表す.
のどんな関数でも三角関数の和で表す
ことができると式(1)は言っている.テイラー展開は任意の関数
を冪乗の和で表したが,フーリェ級数は三角関数の和で表す.
フーリェ級数の何がうれしいの?--とツッコミを入れるひともいるだろう.世の中のどん な周期関数でも三角関数の和で表すことができる--ということ自体,驚くべきことで, 非常に興味深い.実用的な面--工学--を考えると「どんな周期関数でも三角関数を使っ て計算できる」ということは便利この上ない.諸君がよく知っている三角関数の知識で, 図1のようなけったいな関数の解析ができるのである.後で述べ ることになるが,不連続な関数も取り扱うことができる.そのため,フーリェ解析は工学 の諸問題のいたるところで,出現する.交流回路の理論の底には,フーリェ解析があり, 諸君は知らないうちにそれを使っている.電気回路4に 限らずフーリェ解析は線形微分方程式を解くための極めて強力な武器なので,物理学や工 学において光や音,振動の問題にひろく利用されている.近年では,コンピュータグラ フィックスなど分野でもお目にかかる.諸君もフーリェ解析という強力な武器を手に入れ よう.
2.2 フーリエ係数
任意の周期関数をフーリェ級数を使って解析するためには,式 (1)の三角関数の係数--フーリェ係数--2.2.1 準備
フーリェ係数を計算する前に,それに必要な積分を示しておく.同じことをサインの積に対して行うと,
が得られる.残りは,サインとコサインの積である.これは簡単で,
となる.もうひとつ,次の積分
も使う.これで,フーリエ係数を計算する準備ができた.
2.2.2  の計算
の計算
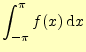 |
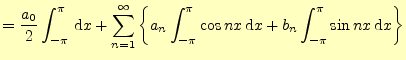 |
|
|
式(8)を使うと
| ||
| (9) | ||
これより,
を計算することにより,
この式をよく見ると,![]() は
は![]() の平均値となっている.電気回路では,この平均
値のことを直流成分と言う.
の平均値となっている.電気回路では,この平均
値のことを直流成分と言う.
2.2.3 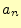 と
と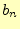 計算
計算
式(1)の両辺にこれより,
を計算することにより,
つぎに,![]() を求めるために,式(1)の両辺に
を求めるために,式(1)の両辺に![]() を乗じ
て区間
を乗じ
て区間
![]() で積分を行う.
で積分を行う.
これより,
を計算することにより,
2.3 収束について
式(1)の両辺が等号で結ばれるためには,ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年12月1日
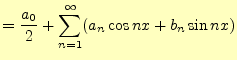
![\includegraphics[keepaspectratio, scale=0.8]{figure/periodic_func.eps}](img63.png)
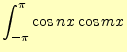
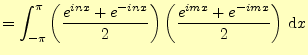
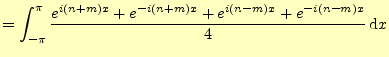
![$\displaystyle =\frac{1}{2}\int_{-\pi}^{\pi}\left[\cos(n+m)x+\cos(n-m)x\right]\,\mathrm{d}x$](img77.png)
![$\displaystyle =\begin{cases}\frac{1}{2}\left[\frac{\sin(n+m)x}{n+m}+x\right]_{\...
...n(n+m)x}{n+m}+\frac{\sin(n-m)x}{n-m}\right]_{\pi}^{-\pi} & (n\ne m) \end{cases}$](img78.png)