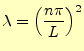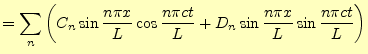1 本日の学習内容

1.1 これまでの復習

図1に示すように$x$軸と垂直な弦の振動の方程式を考える．$x$軸か らの弦の変位を$y(x,t)$とする．場所$x$と時刻$t$を決めたら弦の変位が決まるので，変 位は$y(x,t)$と表すことができる．弦の変位は$y(x,t)$は，弦の長さ$L$に比べて十分小 さい場合，次の偏微分方程式が成り立つ．

$$\if 12 \cfrac{\partial y}{\partial t} \else \cfrac{\partial^{2} y... ... x} \else \cfrac{\partial^{2} y}{\partial x^{2}}\fi \qquad(c^2=T/\rho,\,c\ge 0)$$ (1)

これを波動方程式と言う．

図 1: 弦の振動の様子．

波動方程式(1)--偏微分方程式のひとつ--の解を，

$$y(x,t)=X(x)T(t)$$ (2)

とそれぞれの変数の関数の積の形になると仮定する．これを変数分離形と言う．この仮定 した解を元の偏微分方程式に代入する．すると，

$$X(x)T^{\prime\prime}(t)=c^2X^{\prime\prime}(x)T(t)$$ (3)

が得られる．これは，

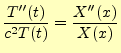$$\frac{T^{\prime\prime}(t)}{c^2T(t)}=\frac{X^{\prime\prime}(x)}{X(x)}$$ (4)

となる．この左辺は時刻$t$のみの関数で，右辺は場所$x$のみの関数である．これが等し いということは，両辺の値は定数でなくてはならない．この定数を$-\lambda$とすると，

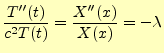$$\frac{T^{\prime\prime}(t)}{c^2T(t)}=\frac{X^{\prime\prime}(x)}{X(x)}=-\lambda$$ (5)

となる．これを整理すると，

$$X^{\prime\prime}(x)+\lambda X(x)=0$$ (6)

$$T^{\prime\prime}(t)+\lambda c^2T(t)=0$$ (7)

という連立常微分方程式になる．弦の振動の場合，図1に示すように 弦の両端で固定されている．固定されている部分では，弦の変位$y(x,t)$はゼロである． したがって，

$$X(0,t)=0 X(L,t)=0$$ (8)

である．この条件--境界条件--を満たすことができるのは，

$$X(x)=B_n\sin\frac{n\pi x}{L} \lambda=\left(\frac{n\pi}{L}\right)^2$$ (9)

である．時刻の項の常微分方程式(7)は，

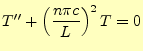$$T^{\prime\prime}+\left(\frac{n\pi c}{L}\right)^2T=0$$ (10)

となる． $(n\pi c/L)^2$は正の実数であるので，一般解は

$$T(t)=a_n\cos\frac{n\pi ct}{L}+b_n\sin\frac{n\pi ct}{L}$$ (11)

となる．空間および時刻の常微分方程式から得られた解を元の仮定した解 (2)に代入すると

$$y_n(x,t)= C_n\sin\frac{n\pi x}{L}\cos\frac{n\pi ct}{L}+ D_n\sin\frac{n\pi x}{L}\sin\frac{n\pi ct}{L}$$ (12)

となる．元の波動方程式は線形なので，重ね合わせの原理が成り立つ．すなわち，解は

$$y(x,t) =\sum_n y_n(x,t)$$

$$=\sum_n\left(C_n\sin\frac{n\pi x}{L}\cos\frac{n\pi ct}{L}+ D_n\sin\frac{n\pi x}{L}\sin\frac{n\pi ct}{L}\right)$$ (13)

と書き表すことができる．

1.2 本日の学習内容

本日は，波動方程式(1)のに初期条件を組み込む方法を学習する．教科書  [1]では，p.250-251の範囲である．ただし，教科書では初期条件とは言 わないで境界条件としている．同じことではあるが，電気の習慣に従うことにする．本日 のゴールは，次のとおりとする．

• 初期条件や境界条件の意味が分かる．
• 微分方程式の一般解に，初期条件や境界条件を取り込む方法が分かる．

具体的には，波動方程式の解である式(13)の$C_n$や$D_n$の値を決め る．
ホームページ: Yamamoto's laboratory
著者: 山本昌志