1 本日の学習内容
1.1 先週までの復習
1.1.1 フーリエ変換
フーリエ変換(Fourier transform)は,時間情報を周波数情報に変換している.すなわち, 時刻の関数で振幅が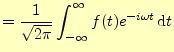 |
(1) | |
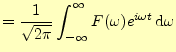 |
(2) |
この式は,次のように理解する.
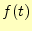 の
の
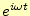 成分--すなわち角振動数
成分--すなわち角振動数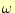 の成分の波--
の成分の波--
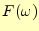 は,ベクトルの内積を用いて成分を見出すように,関数を定義域で乗じて積
分を行う.
は,ベクトルの内積を用いて成分を見出すように,関数を定義域で乗じて積
分を行う.
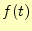 は,周波数毎の振幅
は,周波数毎の振幅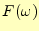 にその波
にその波
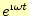 を加えあわせた
ものである.
を加えあわせた
ものである.
1.1.2 導関数のフーリエ変換
導関数のフーリエ変換は,電気では極めて重要なのでもう一度,話しておく.導関数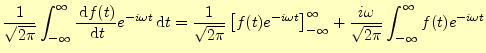 |
(3) |
が得られる.自然界の物理量
である.なぜならば,無限に続く波は存在しないからである.したがって,この式の右辺 の第一項はゼロとなり,導関数のフーリエ変換は,
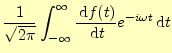 |
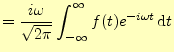 |
|
| (5) |
となる.ようするに導関数のフーリエ変換は,元の関数のフーリエ変換の
2階の導関数のフーリエ変換も考えてみよう.同じように部分積分の公式を使うと,
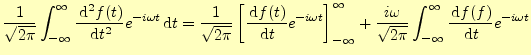 |
(6) |
となる.式(4)から,
となる.同じ計算を進めると,
となる.
1.2 本日の学習内容
本日の内容は,教科書から離れてる.本日のゴールは次のとおりである.- フーリエ変換を利用して電気回路のインピーダンスが求められる.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年2月22日