3 電気回路に応用
3.1 導関数のフーリエ変換
導関数のフーリエ変換は,非常に重要で電気の問題にしばしば表れる.多分,諸君は知ら ないうちにそれを使っている.ここで,ちゃんとした話としておこう.
導関数
![]() のフーリエ変換を
のフーリエ変換を![]() とする.部分積分を利用すると,
とする.部分積分を利用すると,
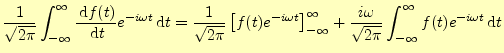 |
(20) |
が得られる.自然界の物理量
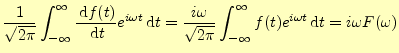 |
(21) |
となる.ようするに導関数のフーリエ変換は,元の関数の
となる.
3.2 RL回路
図9のRL直列回路のインピーダンスを考える.インダクタンスを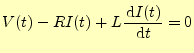 |
(23) |
となる.ただし,電源の電圧は電流の流れる方向を正としている.電源電圧は時間ととも に変化する.それにしたがい回路に流れる電流も変化する.これの両辺に
式(23)を使って,整理すると
| (25) |
となる.ここで,
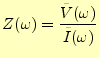 |
(26) |
と定義できる.したがって,図9の電源から見たインピーダンスは, 式(25)より,
| (27) |
となる.電気回路でいつも見る式である.諸君は知らず知らずのうちにフーリエ変換を使っ ていたのである.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年2月22日
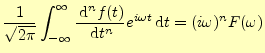
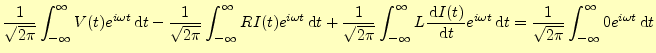
![\includegraphics[keepaspectratio, scale=1.0]{figure/LR_series.eps}](img120.png)