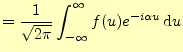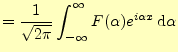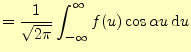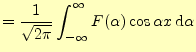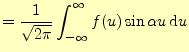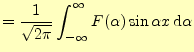1 本日の学習内容

1.1 先週までの復習

1.1.1 フーリエ級数

区間$[-L,L]$で定義された関数$f(x)$は，

$$f(x) =\frac{a_0}{2} +\sum_{n=1}^{\infty}\left[ a_n\cos \frac{n\pi x}{L} +b_n\sin \frac{n\pi x}{L} \right]$$ (1)

$$\quad a_n=\frac{1}{L}\int_{-L}^{L}f(x)\cos \frac{n\pi x}{L} \,\ma... ...qquad \quad b_n=\frac{1}{L}\int_{-L}^{L}f(x)\sin \frac{n\pi x}{L} \,\mathrm{d}x$$

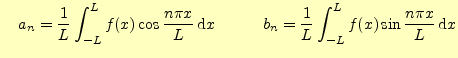のようにフーリエ級数で表すことができる．どんな関数でも，$\sin x$と$\cos x$の和で 表すことができる．

三角関数と指数関数は，オイラーの公式で関係づけることができる．この公式を利用する と，式(1)は，指数関数で表したフーリエ級数は

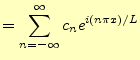$$f(x) =\sum_{n=-\infty}^{\infty}c_n e^{i(n\pi x)/L}$$ (2)

$$c_n=\frac{1}{2L}\int_{-L}^L f(x)e^{-i(n\pi x)/L}\,\mathrm{d}x$$

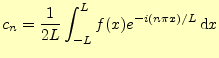1.1.2 フーリエ変換

区間 $[-\infty,\infty]$で定義された関数$f(x)$は，

$$F(\alpha) =\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(u)e^{-i\alpha u}\,\mathrm{d}u$$ (3)

$$f(x) =\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}F(\alpha)e^{i\alpha x} \,\mathrm{d}\alpha$$ (4)

とフーリエ変換とフーリエ逆変換を使って表すことができる．もし，関数$f(x)$が偶関数 であれば，

$$F(\alpha) =\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} f(u)\cos\alpha u\,\mathrm{d}u$$ (5)

$$f(x) =\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} F(\alpha)\cos\alpha x\,\mathrm{d}\alpha$$ (6)

となる．これは，フーリエ余弦変換と逆フーリエ余弦変換と呼ばれる．一方，関数$f(x)$ が奇関数であれば，

$$F(\alpha) =\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} f(u)\sin\alpha u \,\mathrm{d}u$$ (7)

$$f(x) =\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}F(\alpha)\sin\alpha x \,\mathrm{d}\alpha$$ (8)

これは，フーリエ正弦変換と逆フーリエ正弦変換と呼ばれる．

1.2 本日の学習内容

本日の内容は，教科書から離れてる．本日のゴールは次のとおりである． -4pt

• フーリエ変換のイメージが分かる．
• フーリエ変換を電気回路に応用できる．

フーリエ積分やフーリエ変換の実用面については，来週の講義で述べる．
ホームページ: Yamamoto's laboratory
著者: 山本昌志