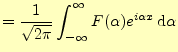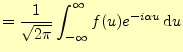2 フーリエ積分
2.1 フーリエ級数
これまで学習してきたように,次のような関数はフーリエ級数で表すことができる. -4pt- 周期的に繰り返す関数
- 有限な区間で定義された関数
![$\displaystyle =\frac{a_0}{2} +\sum_{n=1}^{\infty}\left[ a_n\cos \frac{n\pi x}{L} +b_n\sin \frac{n\pi x}{L} \right]$](img6.png) |
(1) | |
ただし,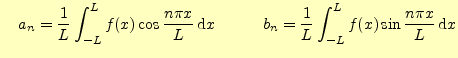 |
のようにフーリエ級数で表すことができる.
2.2 フーリエ積分
先に示したように,フーリエ級数は有限な区間が得られる.ここで,
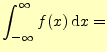 有限の値 有限の値 |
(3) |
とするならば,式(2)の右辺の第一項はゼロに収束する2.なぜならば,
| (4) | ||
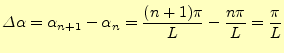 |
(5) |
とおく.すると,
となる.ここで,
とおく.すると,式(6)は,
となる.この右辺はリーマン和の極限--普通の積分--の形になっている.したがって,
と書くことができる.これまでの話をまとめると,次のようになる.
フーリエ積分1
区間
|
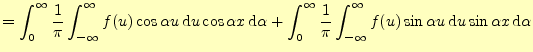 |
||
![$\displaystyle =\frac{1}{\pi}\int_0^{\infty}\int_{-\infty}^{\infty} f(u)\left[ \...
... u\cos\alpha x+\sin\alpha u\sin\alpha x \right] \,\mathrm{d}u\,\mathrm{d}\alpha$](img40.png) |
||
|
三角関数の加法定理を使うと
| ||
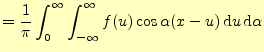 |
(11) | |
がえられる.これもフーリエ積分である.
フーリエ積分2
区間
|
2.3 フーリエ積分(指数関数形)
式(11)から,指数関数を用いたフーリエ積分を求める.その 計算をするときに,オイラーの公式より導くことができる.ここでは,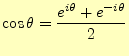 |
(13) |
を用いる.
この式を使うと,式(11)は次のように変形できる.
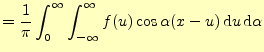 |
||
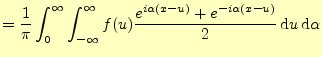 |
||
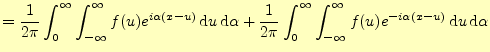 |
||
|
右辺第二項を
| ||
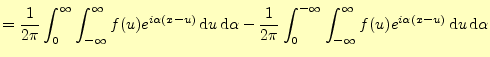 |
||
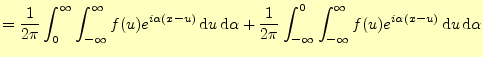 |
||
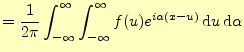 |
(14) | |
この式は,一般には次のように変形されて使われることが多い.
この式もまた,フーリエ積分の別の形である.他のフーリエ積分に比べると式が単純であ ること,また次のフーリエ変換との関係が深いことから,これがもっとも重要である.
フーリエ積分3
区間
|
2.4 注意
ここまでの話は,教科書 [1]のp.239-242に対応する.しかし,教科書で は等号(ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年1月19日
![$\displaystyle f(x)=\frac{1}{2L}\int_{-L}^{L}f(x)\,\mathrm{d}x+\frac{1}{L}\sum_{...
...sin \frac{n\pi x}{L}\int_{-L}^{L}f(u)\sin \frac{n\pi u}{L}\,\mathrm{d}u \right]$](img15.png)
![$\displaystyle f(x)=\lim_{\varDelta\alpha\to 0} \frac{\varDelta\alpha}{\pi}\sum_...
...in(\alpha_n x)\int_{-\infty}^{\infty} f(u)\sin(\alpha_n u)\,\mathrm{d}u \right]$](img24.png)
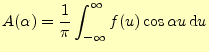
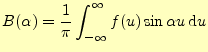
![$\displaystyle =\lim_{\varDelta\alpha\to 0}\varDelta\alpha\sum_{n=1}^{\infty}\left[ \cos(\alpha_n x)A(\alpha_n) +\sin(\alpha_n x)B(\alpha_n) \right]$](img28.png)
![$\displaystyle =\lim_{\varDelta\alpha\to 0}\sum_{n=1}^{\infty}\left[ \cos(\alpha...
...)A(\alpha_n)\varDelta\alpha +\sin(\alpha_n x)B(\alpha_n)\varDelta\alpha \right]$](img29.png)
![$\displaystyle =\lim_{\varDelta\alpha\to 0}\left[\sum_{n=1}^{\infty} A(\alpha_n)...
...a\alpha +\sum_{n=1}^{\infty} B(\alpha_n)\sin(\alpha_n x)\varDelta\alpha \right]$](img30.png)
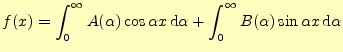
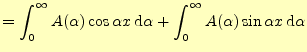
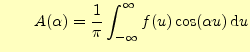
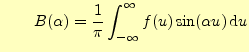
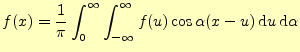
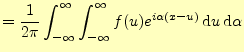
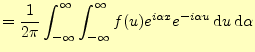
![$\displaystyle =\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\left[ \frac{1}{\sqr...
...{\infty} f(u)e^{-i\alpha u}\,\mathrm{d}u \right]e^{i\alpha x}\,\mathrm{d}\alpha$](img59.png)