2 定常電流と保存即
2.1 電流とは
電磁場を統一したマクスウェルの方程式3が発表されたのは、1864年のことである。この式から、運動する電荷が 磁場を作ると予見されていたが、それを実験的に確認することは困難であった。1878年ア メリカの物理学者ローランドが、実験によりそれを確認した。ここで初めて、電荷の流れ により電流が生じることが確かめられた。
帯電した円盤を回転させて、それにより磁石が力を受けることを実験的に確認したのであ
る。このときの磁場の測定精度は、地磁気の![]() 程度とのことである []。それにしても、130年くらいまえに、このような精度で実験がなされた
ことに驚きである。この実験は、全てではないにしてもマクスウェルの方程式の正しさを
証明したと言えるだろう。その10年度、ヘルツの電磁波の確認により、その方程式は確固
たる地位を築いた。
程度とのことである []。それにしても、130年くらいまえに、このような精度で実験がなされた
ことに驚きである。この実験は、全てではないにしてもマクスウェルの方程式の正しさを
証明したと言えるだろう。その10年度、ヘルツの電磁波の確認により、その方程式は確固
たる地位を築いた。
電荷の流れが電流を作ることを諸君は既に知っているだろう。水の分子の流れが水流を作 るようにである。電流の場合、電荷は正負があり、正の電流の流れる方向を電流の方向と 定めている。実際の回路では、負の電荷を帯びた電子が電流を担う。従って、電子の流れ と電流の流れは逆になっている。水にたとえるならば、水の分子の流れと、水流の流れが 逆になっているようなものである。多少不便はあるが、歴史的な経緯で、そのようになっ てしまった。電子よりも先に電流が発見され、その方向が決められたことによる。
導線に流れる電流は、
- 断面を単位時間に通過する電荷量
である。ここで、
導線に流れる電流![]() は場の量としてふさわしくない。これは、導線の直径にわたっての
トータルの性質を表しているからである5。そこで、場の量として電流密度6
は場の量としてふさわしくない。これは、導線の直径にわたっての
トータルの性質を表しているからである5。そこで、場の量として電流密度6
![]() を定義することにする。電流
を定義することにする。電流![]() は明らかにスカラー量で
ある。これはある断面
は明らかにスカラー量で
ある。これはある断面![]() を通り抜ける単位時間あたりの電荷量となる。ある微小断面積
を通り抜ける単位時間あたりの電荷量となる。ある微小断面積
![]() 、その法線ベクトルを
、その法線ベクトルを
![]() 、微小電流量
、微小電流量
![]() とすると
とすると
となるであろう。なぜならば、図1に示すように、どんな
このことから、ある断面![]() を貫く電流は、
を貫く電流は、
と表すことができる。
2.2 積分形の定常電流の保存則
ここでは、電流密度と電荷の関係を考える。そのため、風船のように体積をもつ閉じた系 を考える。この系の表面で先ほどの積分、式(3)を適用する。この積分が 正の場合、それはこの体積中に電流が注入されることになる。すると、電流は電荷の流れなの で、電荷が時間とともにどんどん貯まることになる。あるいは、電荷がその体積中で消滅 するかである。いままで、電荷の消滅は観測されていない7ので、後者は考えないものとする。従って、先の式 (3)が正の場合、その中に電荷が貯まることになる。一方、負の場合は その逆で電荷が減るのである。ゼロの場合、正味の電荷量に変化は無いことになる。
式(1)を考えている系の表面で積分すると、系から出て
いく電流![]() が分かる。それは、
が分かる。それは、
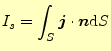 |
(4) |
となる。この電流は、そこを通して出ていく時間あたりの電荷量
| (5) |
となる。このことから、
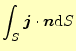 |
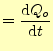 |
|
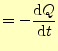 |
(6) |
である。これは、外部に向かって電流が流れ出ると(左辺)、内部の電荷量が減少すると言っ ている。この式は電荷の保存の法則を、式で表したものである。電荷量
となる。これが式で書いた電荷保存の法則(積分形)である。
場の量である電流密度
![]() も電荷密度
も電荷密度![]() も、場所と時間
も、場所と時間
![]() の関
数である。時刻とともに、これらの場が変化しないとき定常状態と呼ぶ。従って、定常状
態では、
の関
数である。時刻とともに、これらの場が変化しないとき定常状態と呼ぶ。従って、定常状
態では、
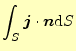 |
(8) |
となる。定常状態では、閉じた系のトータルの電流はゼロである。これは、内部で電荷量 の変動が無いことを示している。
2.3 微分形の定常電流の保存則
諸君はガウスの発散定理をよく知っている。式 (7)の右辺をガウスの発散定理を用いて書き直し、 左辺は微分と積分の順序を交換する。そうすると、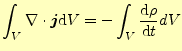 |
(9) |
となる。この式は、いつでもどのような
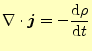 |
(10) |
となる必要がある。これを、微分形の電荷保存の法則という。電流密度の発散は、電荷密 度の変化の割合に等しいと言っている。積分形に比べて、何を言っているかは分かりにく いが、理論的に話を進めるときには微分形の方が便利である。
この場合、定常状態は、
| (11) |
と表せる。定常状態では電流の発散は無い。これも積分形に比べて、何のことか分かりに くい。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月24日
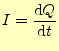
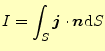
![\includegraphics[keepaspectratio, scale=1.0]{figure/current_density.eps}](img26.png)
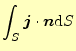
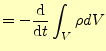
![\includegraphics[keepaspectratio, scale=0.7]{figure/div_minus.eps}](img46.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/div_zero.eps}](img49.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/div_plus.eps}](img52.png)