5 コンデンサーと静磁場のエネルギー
5.1 導体表面の電荷分布
図3のように絶縁体の棒を帯電させて、金属球に近づけると、クー ロン力により金属中の自由電子は移動し、その結果、電荷分布の偏りが生じる。この場合、金属 中の電場がゼロになるように、自由電子はとても早く移動する。もし、電場がゼロでない とすると、その作用により自由電子は電場をゼロにするように移動する。すなわち、電場がゼロにな るまで電子は移動し続けるのである。この電場がゼロという状態は、外部の帯電させた絶縁体が作 る電場と金属内の自由電子が作る電場をあわせてゼロということである。すなわち、金属 内の自由電子は、外部からの電場をキャンセルするように移動するのである。内部の電場の状態は分かった。金属の表面ではどうなるか?。金属の表面での接線方向の 電場はゼロになる。もし、接線方向に電場があると、ここでも電子はそれをゼロにするよ うに移動する。従って、接線方向の電場はゼロにならなくてはならない。従って、金属の 表面では電場は法線方向のみとなる。金属から電子が飛び出さないのは、また別の力が働 くからである。
金属の表面の法線方向の電場は、積分系のガウスの法則から導くことができる。金属表面
の法線方向の電場を![]() とする。金属内部には電場はないので、この法線方向の電場は
外側のみにある。そして、金属表面の電荷密度を
とする。金属内部には電場はないので、この法線方向の電場は
外側のみにある。そして、金属表面の電荷密度を![]() とする。ここで、表面の微少面
積
とする。ここで、表面の微少面
積![]() を考えると、ガウスの法則は、
を考えると、ガウスの法則は、
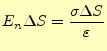 |
(25) |
となる。従って、
である。これが、表面電荷密度と表面の電場の関係である。
| コーヒーブレイク
余談であるが、金属が光沢があるのは、この自由電子の作用である。光の電場が金属内に
入り込もうとすると、自由電子は非常に早く移動して、それを阻止する。光の電場と同期
して、電子が移動することになる。その移動により新たに電場がつくられ、入射光と反対
方向に電磁波(光)を放射する事になる。これが反射光となり、金属は光沢を持つのである。
一般に光るものは、自由電子がふんだんにあり、電気を通しやすい。
さらにこの自由電子は熱を伝える働きもする。金属の熱伝導率が高いのも、大量に自由電 子があるからである。熱と光と全く異なった現象であるが、同じ自由電子が関与してい るのはおもしろいことである。 |
5.2 コンデンサー
2つの導体を近づけて、各々に導線を接続させるとコンデンサーができあがる(図 5)。2つの金属に正負が反対で等量の電荷(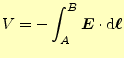 |
(27) |
は積分の経路によらない。2つの間の空間で、この積分が経路によらないのは以前示した とおりである。加えて、金属表面の接線方向にも電場が無い。従って、この積分(電圧)は 経路に依存しない。諸君は、これまでの学習や実験で電圧は経路によらないことは十分承 知しているはずである。
また、電荷の分布の形が変わらなければ、電圧は電荷量に比例する。重ね合わせの原理が 成り立つからである。従って、次のような量
が定義できるはずである。この
ここで、実際のコンデンサーの容量を求めてみよう。問題を簡単にするために、図
6の平行平板コンデンサーを考える。下側の導体には![]() が、上側に
は
が、上側に
は![]() の電荷があるとする。通常、コンデンサーでは、導体間隔(x方向)に比べて、水平
方向(y,z方向)には十分広い。そして、一様に電荷は分布している。そのため、電場は、
の電荷があるとする。通常、コンデンサーでは、導体間隔(x方向)に比べて、水平
方向(y,z方向)には十分広い。そして、一様に電荷は分布している。そのため、電場は、
![]() と考えることができる。また、導体の間の空間では、ガウスの法則が
成り立つので2、
と考えることができる。また、導体の間の空間では、ガウスの法則が
成り立つので2、![]() は至る所で同じ値にな
る。その値は、式(26)より、
は至る所で同じ値にな
る。その値は、式(26)より、
| (29) |
となる。ここで、
電圧は、これを積分すれば良いので、
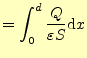 |
||
| (30) |
となる。したがって、平行平板コンデンサーの容量は式(28)か ら、
となる。これは、よく知られた式である。大きな容量のコンデンサーを作るためには、導 体の間隔
5.3 コンデンサーに蓄えられるエネルギー
コンデンサーの両電極に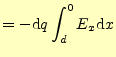 |
||
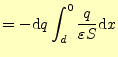 |
||
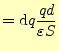 |
||
| (32) |
となる。
コンデンサーの両電極に![]() と
と![]() を蓄えるために必要な外部からの仕事の総量は、式
(32)を0〜
を蓄えるために必要な外部からの仕事の総量は、式
(32)を0〜![]() まで積分する事により求められる。仕事の総量は、
まで積分する事により求められる。仕事の総量は、
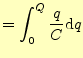 |
||
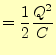 |
(33) |
である。外部からの仕事は、コンデンサーの内部にエネルギーとして蓄えられる。両電極 にモーターを接続すると、それを回すことができ、蓄えられたエネルギーを取り出すこと ができる。コンデンサーに蓄えられたエネルギーは静電エネルギー
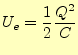 |
(34) |
のように記述する。これは、式(28)を用いて
| (35) |
と書かれるのが普通である。これで、コンデンサーをある電圧で充電したとき、そこに蓄 えられているエネルギーが計算できる。
| 容量の定義 | |||||
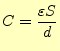 |
容量の計算方法 | ||||
| 蓄積エネルギー |
暗記している。
5.4 静電場のエネルギー
コンデンサーのエネルギーはどこに蓄えられているのであろうか?。近接作用の考え方(場 の考え方)を取り入れると、それは両電極の空間に静電エネルギーあると考える。それで は、コンデンサーの蓄積エネルギーを場の式に直してみよう。そのために、電場を式 (26)を用いて、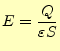 |
(36) |
と書き換えておく。これと、コンデンサーの容量の式(31)を用いると、 蓄積エネルギーは、
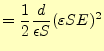 |
||
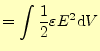 |
(37) |
と書き換えられる。
これから、コンデンサー内部でのエネルギー密度は
![]() と考えても良
いだろう。これは、一般化できて、電場のエネルギー密度
と考えても良
いだろう。これは、一般化できて、電場のエネルギー密度![]() は
は
| (38) |
と計算できる。この式は、時間的に変化する場でも適用できる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月24日
![\includegraphics[keepaspectratio, scale=0.8]{figure/seiden_yudo.eps}](img66.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/gauss_int_surface.eps}](img67.png)
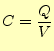
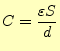
![\includegraphics[keepaspectratio, scale=0.7]{figure/two_plate.eps}](img88.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/capaciter.eps}](img89.png)