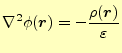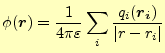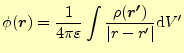4 静電ポテンシャルとポアッソン方程式

電場 $\boldsymbol{E}$は、発散を表す式(9)と回転を示す式 (15)の微分方程式を解けば計算できるが、大変である。一般 にベクトルの方程式を計算するのは大変である。一方、スカラー場$\phi$を計算し、その 勾配から電場を計算するのは比較的簡単である。

それでは、スカラー場が満たす方程式を考えよう。スカラー場の勾配が電場、 $\boldsymbol{E}=-\nabla\phi$となる。また、電場の発散が電荷密度、 $\nabla\cdot\boldsymbol{E}=\rho/\varepsilon$である。したがって、

$$\nabla\cdot\left(-\nabla\phi\right)=\frac{\rho}{\varepsilon}$$ (20)

となり、スカラーポテンシャルは

$$\nabla^2\phi(\boldsymbol{r})=-\frac{\rho(\boldsymbol{r})}{\varepsilon}$$ (21)

となる。この式を「ポアソン方程式」と言う。また、領域に電荷がない場合、

$$\nabla^2\phi=0$$ (22)

となり、この式を「ラプラス方程式」と言う。静電場の場合、一般的にはポア ソン方程式で、電荷が無い特別な場合「ラプラス方程式」となる。

ポアソン方程式(21)は、スカラーの方程式なので解きやすい。 解きやすいといっても、これを直接計算するのは、そんなに易しいことではない。そこで、 直感的にこの微分方程式の解(ポテンシャル)を求めることにする。電荷が点電荷の場合の この微分方程式のポテンシャルは、すでに分かっており、式 (19)のとおりである。

次に複数の点電荷がつくるポテンシャルを考える。この場合、電場は重ね合わせの原理が成り立つの で、

$$\phi(\boldsymbol{r})=\frac{1}{4\pi\varepsilon}\sum_i\frac{q_i(\boldsymbol{r_i})}{ \vert r-r_i\vert}$$ (23)

となる。ここで、不連続な点電荷$q_i$を連続的な電荷密度$\rho$に置き換えると、和は 積分に置き換わる。従って、

$$\phi(\boldsymbol{r})=\frac{1}{4\pi\varepsilon}\int\frac{\rho(\boldsymbol{r^\prime})}{ \vert r-r^\prime\vert}\mathrm{d}V^\prime$$ (24)

となる。これが、ポアソン方程式(21)の解である。無限遠を基 準($\phi=0$)としたときの任意の場所のポテンシャルを示す。

ポテンシャルが分かるとなにがうれしいか?。それは、ポテンシャルはそれだけでも電圧 という物理的な意味がある。それだけでもうれしいが、それを微分することにより電場も 求められるのである。ポテンシャルが分かると静電場の問題は解けたと言える。

ホームページ: Yamamoto's laboratory
著者: 山本昌志