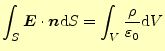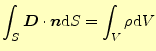3 ガウスの法則
電場を導入することにより近接作用の考えを導入したつもりでいた。しかし、式 (6)や(8)、(9)は、まだ 満足できない。遠隔地にある電荷が電場を作っている式になっている。近接作用を考える と、その場所の電場はその周りからのみ作用を受けるべきである。そのためには、式を微 分系に直すのが良いだろう。それぞれの式は正しいので、それを上手に使い微分形の式を 導く。3.1 積分形のガウスの法則
3.1.1 球の場合(電荷は内側)
点電荷となる。この式の言っていることは、
- 球の表面の電場
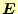 の面積分(左辺)は、電荷量
の面積分(左辺)は、電荷量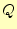 を誘電率
を誘電率
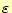 で
割った値に等しい。そして、これは球の半径に依存しない。
で
割った値に等しい。そして、これは球の半径に依存しない。
3.1.2 任意形状の場合(電荷は外側)
次に図8のように、任意の形状の閉じた領域の外側に電荷がある場合 を考える。球形領域の微少表面のが分かる。この微少面積の積分は、球形領域の半径に依存しないから、これが成り立つ。
次に、球形領域と任意形状の領域の関係を調べる。先ほどの図では分かり難いので、図 9のように添字1の領域を拡大する。まずは、球形領域であ るが、この場合法線ベクトルと電場の方向は等しいので、
となる。任意領域では、
となる。図から明らかなように、それぞれの微少面積は
の関係がある。これら、3つの式、(12)と(13)、 (14)から、
が導かれる。この式は、立体角が等しい場合、電場の面積分は面の向きに依存しないと言っ ている。球のように電場と法線方向が一致した場合と図に示した任意形状のように一致し ない場合でも面積分の値はおなじである。これは、面が傾いた分だけ面積が大きくなる割 合と内積が減少する割合が等しく、それぞれの効果をキャンセルするからである。
図8の添え字2の領域でも、式(15)の関係は成り立つ。 従って、添字1と2の領域の式(15)と式(11)から、
が成立する。この式は、電荷からみた同じの見込み角の添字1と添字2の領域の積分はキャ ンセルすると言っている。
このことは、閉じた任意形状の全ての部分で成り立つので、全てキャンセルする相手があ る。ということは、任意形状の外側にあるとき、表面での電場の面積分はゼロになると言 うことである。式で表すと
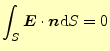 電荷がSの外側にある場合 電荷がSの外側にある場合 |
(17) |
となる。
3.1.3 任意形状の場合(電荷は内側)
最後に任意形状で、電荷がその内側にある場合を考える。これは、図 8の中に電荷を入れるのであるが、図10のように考え る。積分領域を以下の3つの部分に分ける。複素関数の積分を思い出せ。- 領域の中にあり、電荷を囲んだ球形の領域の表面を
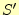 とする。
とする。
- 元の任意の囲まれた領域の表面を
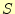 とする。
とする。
- この2つの領域を接続する部分を連結部とする。
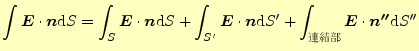 |
(18) |
となる。
図10に示した部分の表面で電場の面積分を行うが、電荷![]() は連結部
を通して外側にあるので、
は連結部
を通して外側にあるので、
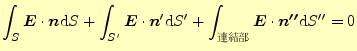 |
(19) |
となる。ここで、複素関数の積分を行ったのと同じテクニックをつかう。連結部のパイプの直径を極限まで 小さくする。すると、そこの積分は寄与は無くなり
となる。ここで、内部の領域
である。
最終的に我々が知りたい閉じた任意形状の領域に点電荷![]() がある場合、その表面での電
場
がある場合、その表面での電
場
![]() の面積分である。それは、式(21)と
(20)から
の面積分である。それは、式(21)と
(20)から
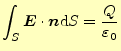 領域内部に点電荷 領域内部に点電荷 |
(22) |
となる。これは、領域内部に点電荷が無い場合の式(16)も包含して いる。従って、点電荷が作る電場の面積分に関する式は (22)で十分である。この式の言っていることは、
- 点電荷を任意の閉じた領域で囲むと、その表面の電場の面積分は、その電荷量を誘
電率
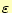 で割った値に等しい。
で割った値に等しい。
3.1.4 任意形状の場合(複数の点電荷と連続分布)
電場は重ね合わせの原理が成り立つことから、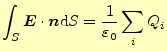 領域内部の加算 領域内部の加算 |
(23) |
は明らかである。
密度![]() で連続的に電荷が分布している場合は、式
(24)の和を積分に変えれば良い。
で連続的に電荷が分布している場合は、式
(24)の和を積分に変えれば良い。
体積積分の領域は、閉じた領域内部である。この式を積分形のガウスの法則という。この 式の言っていることは、
- ある領域に含まれる電荷量は、その領域の表面で電場を面積分すれば分かる。
ガウスの定理は電束密度
![]() というベクトル場
というベクトル場
| (25) |
を定義して、
と書かれることも多い。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月24日
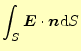
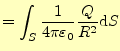
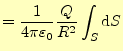
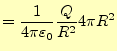
![\includegraphics[keepaspectratio, scale=1.0]{figure/gauss_Q_kyu.eps}](img70.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/denka_soto.eps}](img80.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/denka_soto_kakudai.eps}](img81.png)
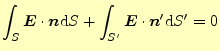
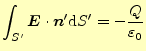
![\includegraphics[keepaspectratio, scale=1.0]{figure/denka_naka.eps}](img97.png)