2 静電力と静電場
2.1 静電力の式の分割
最初に遠隔作用と近接作用の復習を行う。真空中に置かれた2つの電荷の間に働く力の大きさを示すクーロンの法則(Coulomb law)は 以前示したように、と書くことができる。この式のそれぞれ記号とその単位については、表 1に示している。
この力は、2通りの見方ができる。遠隔作用(action at distance)と近接作用(action
through medium)である。![]() の場合の
の場合の![]() に働く力を考える。まずは、遠隔作用であるが、
その概念を図 1に示す。電荷
に働く力を考える。まずは、遠隔作用であるが、
その概念を図 1に示す。電荷![]() が
が![]() を引っ張っているの
である。それだけの話であるが、なにもない空間を通して力が作用しているのである。何
もない空間を通して力が作用するということはなかなかイメージできない。このことにつ
いては文献 [1] 2には次のように書かれている。
を引っ張っているの
である。それだけの話であるが、なにもない空間を通して力が作用しているのである。何
もない空間を通して力が作用するということはなかなかイメージできない。このことにつ
いては文献 [1] 2には次のように書かれている。
ニュートンが、太陽-地球間、地球-月間に引力が働くと語ったとき、何もない真空の空 間を隔てて力が、それも瞬間的に及ぼされる - 遠隔作用 - というそのニュートンの考え方に多くの人が難色を示し、ニュートン自身もこの点ではっ きりとした見解を出せないでいた。特に、日常的に知られる力の大半が、直接的接触に よる圧力や衝撃、あるいはゴムのような弾性体を媒介として伝えられるものであるだけ に、遠隔作用のイメージはえがきにくいものであった。
次に近接作用であるが、そのイメージは図 2である。
![]() があることによる
があることによる![]() が受ける力は先ほどの遠隔作用と同じである。しかし、力の伝わ
り方がことなる。近接作用の場合は2段階で、
が受ける力は先ほどの遠隔作用と同じである。しかし、力の伝わ
り方がことなる。近接作用の場合は2段階で、
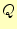 がその周りの空間をゆがめる(場を変化させる)。
がその周りの空間をゆがめる(場を変化させる)。
- 場が変化した結果、その場から
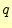 は力を受ける。
は力を受ける。
どちらが正しいかというと、クーロンの法則だけ考えると、どちらも正しいのである。た だし、より進んだ問題を考えると遠隔作用には多くの問題がある。まずは、力が瞬時に伝 わると言うのは、実験の結果から明らかに間違いである。この問題を解決するような遠隔作用 を考えることもできると思われるが、その他いろいろと困難が生じる。そのようなことか ら、遠隔作用の考えはきっぱり捨てて、近接作用を採用した方が困難が少なくて済む。と いうことで、これ以降、全面的に近接作用の考えで進めることにする。
クーロンの法則の式(1)から、近接作用にするためには、
とすればよい。最初は、電荷
2.2 電場の概念
2.2.1 クーロンの法則と電場
この辺は、教科書に書いてあるとおりで、それに沿って説明する。物理で書かれる方程式には、以下の決まりがある。
- 左辺と右辺の単位(次元)が等しい。
- 左辺と右辺が表す量の性質が同一。左辺がスカラー量ならば右辺もスカラー量、 左辺がベクトル量ならば右辺もベクトル量となる。
このような観点から、式(3)を見ると、本当はベクトル量なのにスカラー
量の用に書かれているものがある。力![]() は、明らかにベクトル量である。すると、
式(3)の右辺もベクトル量である必要がある。電荷量の
は、明らかにベクトル量である。すると、
式(3)の右辺もベクトル量である必要がある。電荷量の![]() はスカラー量
なので3、電場
はスカラー量
なので3、電場![]() がベクトル量でなくては
ならい。電場の方向を力の方向と考えると、この考えは良さそうである。
がベクトル量でなくては
ならい。電場の方向を力の方向と考えると、この考えは良さそうである。
電場![]() がベクトル量となると、式(2)の右辺もベクトル量となる
必要がある。
がベクトル量となると、式(2)の右辺もベクトル量となる
必要がある。
![]() は比例定数みたいなものでスカラー量である。電荷
量
は比例定数みたいなものでスカラー量である。電荷
量![]() もスカラー量である。
もスカラー量である。![]() と何か?。これは距離の2乗なので、これもスカラー量で
ある。右辺は全てスカラー量ではないか!!!。何かが間違っている。次のような可能性が
考えられる。
と何か?。これは距離の2乗なので、これもスカラー量で
ある。右辺は全てスカラー量ではないか!!!。何かが間違っている。次のような可能性が
考えられる。
- 式(2)に何か忘れているのか?
- 左辺がベクトル、右辺がスカラーの方程式が許されるのか?
- 電場
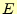 をベクトル量としたことに間違いがあるのか?
をベクトル量としたことに間違いがあるのか?
- 真空中に2つの点電荷を置いたとき、距離の2乗に反比例し、電荷の積に比例した力が働く。
- 力の方向は2つの電荷の延長線上で、電荷の積が負の場合は引力が、正の場合は斥力が働く。
とすれば良い。
この式の添え字の1と2を入れ替えると、
![]() を求めることができる。すると、
を求めることができる。すると、
| (5) |
になっていることが分かるであろう。これを作用反作用の法則と言う。
- [問]
- 作用反作用の法則が成り立たない場合、永久機関が作れる。その永久 機関を考えよ。
力は求まった。![]() が位置
が位置
![]() に作る電場は、
に作る電場は、
となる。
式(6)を一般化して、
![]() に位置にある電荷
に位置にある電荷
![]() ある任意の位置
ある任意の位置
![]() の電場
の電場
![]() は
は
となる。
2.2.2 重ね合わせの原理
いままでは、2つの電荷の間に働く力を問題にしていた。3つ以上の場合はどうなるだろう か?。答えは、それぞれの電荷からによる力のベクトル和である。このことから、電場も ベクトル和になると考えることができる。事実、全ての電荷が作る電場を足しあわせると そこの電場が分かる。このように足しあわせることを重ね合わせの原理と言う。これから、 ある任意の位置となる。この様子を図5に示す。
次に、電荷が連続的に分布していると仮定しよう。位置
![]() での電荷密度を
での電荷密度を
![]() とると、先ほどの和の部分は積分となり、
とると、先ほどの和の部分は積分となり、
と表せる。この様子を図6に示す。
宇宙全体にこの積分を行えば、静電場は分かる。しかし、実際の問題でこの積分を行うこ とはまず無い。単純な場合を除いて、この積分を実行することは大変である。そこで、も う少し簡単に計算する方法を考えることにする。
2.3 自己力
これについての詳細は静電場のエネルギーと絡めて、後の講義で説明する。ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月24日
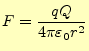
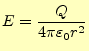
![\includegraphics[keepaspectratio, scale=1.0]{figure/action_at_distance.eps}](img25.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/action_through_medium.eps}](img26.png)
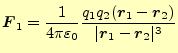
![\includegraphics[keepaspectratio, scale=1.0]{figure/Coulomb_law.eps}](img39.png)
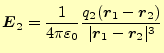
![\includegraphics[keepaspectratio, scale=1.0]{figure/e_field_by_q2.eps}](img45.png)
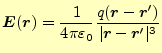
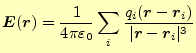
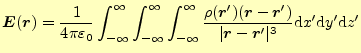
![\includegraphics[keepaspectratio, scale=1.0]{figure/kasane_1.eps}](img57.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/kasane_2.eps}](img58.png)