3 外積 (ベクトル積)
3.1 ベクトル積が現れる演算
角運動量は、「回転中心からの距離| (14) |
である。エネルギーとは異なり、今度は
3.2 ベクトル積の定義
角運動量やトルクなどを取り扱う場合に便利なようにベクトル積を定義する。それは、と書かれる。演算の結果の
| (16) |
とする。ここで、
| (17) |
となる。積の順序を入れ替えると、符号が反対になるのである。内積の場合と異なり、か け算の順序は重要となる。
ベクトル積の幾何学的な意味を考えよう。式(15)の演算は、図
5のようになる。
![]() と
と
![]() で定まる平行四辺形の底面
を
で定まる平行四辺形の底面
を
![]() とすると、高さは
とすると、高さは
![]() となる。従ってその面積は、
となる。従ってその面積は、
![]() と直ちに分かる。これは、
と直ちに分かる。これは、
![]() に等し
い。このことから、
に等し
い。このことから、
![]() のベクトル積は、
のベクトル積は、
![]() と
と
![]() で定まる
平行四辺形の面積を大きさとして、その平行四辺形の平面に垂直な方向のベクトルという
幾何学的な意味があることが理解できる。
で定まる
平行四辺形の面積を大きさとして、その平行四辺形の平面に垂直な方向のベクトルという
幾何学的な意味があることが理解できる。
定義から、単位ベクトル同士のベクトル積の演算は簡単に求めることができる。
![]() 軸の単位ベクトル
軸の単位ベクトル
![]() の演算は、次のとおりである。
の演算は、次のとおりである。
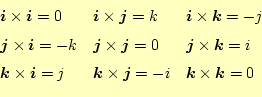 |
これは、
これを使って、ベクトルの成分で考える。ベクトル
![]() と
と
![]() のベクトル積は、
のベクトル積は、
| (19) |
となる。これから、ベクトル積の演算を成分で表すと
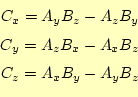 |
となる。この式は、覚えにくいので、行列式を用いて
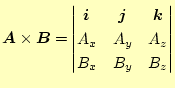 |
(21) |
と表すことがよくある。この行列式を用いた表現は便利なので覚えておく方が良いだろう。
![]() がベクトルになることの証明はしていない。座標軸を回転させた場
合のその成分の振る舞いを考えなくてならない。興味がある者はトライしてみるのが良い
だろう。ここでは示さないが、このベクトル積の計算結果はベクトルになるのはたしかで
ある。
がベクトルになることの証明はしていない。座標軸を回転させた場
合のその成分の振る舞いを考えなくてならない。興味がある者はトライしてみるのが良い
だろう。ここでは示さないが、このベクトル積の計算結果はベクトルになるのはたしかで
ある。
- [練習1]
-
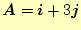 と
と
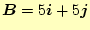 のベクトル積を求めよ。
のベクトル積を求めよ。
- [練習2]
-
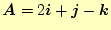 と
と
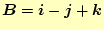 の両方に垂直な単位ベクトル
を求めよ。。
の両方に垂直な単位ベクトル
を求めよ。。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 yamamoto masashi
平成17年5月14日
![\includegraphics[keepaspectratio, scale=1.0]{figure/angular_momentum.eps}](img61.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/vector_product.eps}](img71.png)