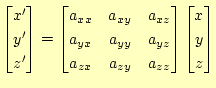2 内積 (スカラー積)

2.1 内積が現れる演算

エネルギーは、「力$\times$距離」とよく表現される。例えば、重力場に質量$m$ の物体 があり、それを垂直に$r$だけ手で移動させたとする。実際には、物体は鉛直方向 に重力により引っ張られており、その力は$mg$である。その力に抗して、手はそれ と同じ大きさで反対方向に力$F$を加え、物体を$r$引き上げたことになる。こ の場合、この物体の位置エネルギー(ポテンシャル)の増加$\Delta U$は、$F r$ となるのは力学で学習したとおりである。

今度は、先ほどと同じ距離で、物体を真横に移動させたとする。この場合、位置エネルギー の変化$\Delta U$はゼロである。また、斜めに移動させた場合は、 $\Delta U=Fr\cos\theta$となる。これは、高さの変化分が、位置エネルギーの変化になるからであ る。手の力の方向は、この3とおりの場合まったく同じで、垂直方向である。この垂直方 向の力$F$と移動方向との角度を$\theta$とすると、3通りとも同じ式

$$\Delta U=Fr\cos\theta$$ (1)

でエネルギーの変化をあらわすことができる。

ちょっと余談であるが、これまで、3通りの方法で物体を移動させた。図を見て分かるよ うに、物体を移動させるとき手にかかる力は同じである。同じ力なのに、移動方向が違う のである。厳密に考えると、移動が始まる瞬間に加速度が生じその力が本当は必要なので あるが、ここでは無視している。ゆっくり、本当にゆっくり移動させたことを考えるので ある。もう少し思考実験を進めると、手と物体との間にばね秤をつけると、力の様子が分 かる。本当にゆっくり動かせば、3通りの移動ともばね秤が示す重さは$m$で力が同じであ ることが分かるであろう。

話は元に戻るが、力と物体の移動量はベクトル量なので $\boldsymbol{F}, \boldsymbol{r}$と書 いたほうが格好良い²。そうすると、位置エネルギーの変化 は、

$$\Delta U=\vert\boldsymbol{F}\vert\vert\boldsymbol{r}\vert\cos\theta$$ (2)

となる。この式の右辺が内積(スカラー積)の演算である。

図 1: 垂直方向への移動

図 2: 水平方向への移動

図 3: 斜めへの移動

2.2 ベクトル量(復習)

スカラー積を学習する前に、ベクトルとスカラーの定義を示しておくのが良いだろう。

前回の授業で示したように、ベクトルの成分は座標軸に依存している。座標軸が異なると、 その3成分は異なる。座標軸を回転させた場合、ベクトルの成分の変換は、座標系の変換 と同じである。具体的には、座標系を $(x, y, z)\rightarrow(x^\prime, y^\prime, z^\prime)$と回転させる。この回転を

$$\begin{bmatrix}x^\prime y^\prime z^\prime \end{bmatrix}= \b... ...a_{zx} & a_{zy} & a_{zz} \end{bmatrix} \begin{bmatrix}x y z \end{bmatrix}$$ (3)

と行列を用いて表現する³。 $(x, y, z)$座標系の時のベクトル $\boldsymbol{A}$の成分を $(E_x, E_y, E_z)$、 $(x^\prime, y^\prime, z^\prime)$座標系では $(E_x^\prime, E_y^\prime, E_z^\prime)$とする。これらの成分の関係は、

$$\begin{bmatrix}E_x^\prime E_y^\prime E_z^\prime \end{bmatri... ... & a_{zy} & a_{zz} \end{bmatrix} \begin{bmatrix}E_x E_y E_z \end{bmatrix}$$ (4)

となる。式(3)と式(4)を見て分かるよう に、回転に対して座標の変換とベクトルの成分の変換は全く同じように取り扱われるので ある。このように座標の回転と同じように、その成分が変換されるものをベクトルと定義 する。これは、ベクトルが、空間に固定された幾何学的な矢と思えば当たり前のことであ る。

2.3 スカラー量

スカラー量は、座標の回転により変化しない量と定義する。たとえば、ベクトルの大きさ の2乗

$$\vert\boldsymbol{E}\vert^2=E_x^2+E_y^2+E_z^2$$ (5)

はスカラー量である。この量は座標系の回転に関係なく一定の値である。ベクトルは空間 に固定された矢であり、その長さの2乗であるから当然のように思える。実際にそれを確 認してみよう。式(3)と式(4)の回転を表 す行列とベクトルを

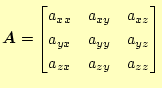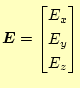$$\boldsymbol{A}= \begin{bmatrix}a_{xx} & a_{xy} & a_{xz} a_{yx} & a_{yy} & a_{yz} a_{zx} & a_{zy} & a_{zz} \end{bmatrix} \boldsymbol{E}= \begin{bmatrix}E_x E_y E_z \end{bmatrix}$$ (6)

と表現する。すると、 $\boldsymbol{E}^\prime=\boldsymbol{A}\boldsymbol{E}$である。そして、 $\vert\boldsymbol{E}\vert^2=\boldsymbol{E}^T\boldsymbol{E}$である。回転後の座標系でのベクトルの大きさの2乗は

$$\vert\boldsymbol{E}^\prime\vert^2 =\boldsymbol{E}^{\prime T}\boldsymbol{E}^\prime$$

$$=\left(\boldsymbol{A}\boldsymbol{E}\right)^T\boldsymbol{A}\boldsymbol{E}$$

$$=\boldsymbol{E}^T\boldsymbol{A}^T\boldsymbol{A}\boldsymbol{E}$$

$$\boldsymbol{A}^t=\boldsymbol{A}^{-1}$$

$$=\boldsymbol{E}^T\boldsymbol{A}^{-1}\boldsymbol{A}\boldsymbol{E}$$

$$=\boldsymbol{E}^T\boldsymbol{E}$$

$$=\vert\boldsymbol{E}\vert^2$$ (7)

となる。回転前後で、ベクトルの大きさは変化しない。従って、これはスカラー量である。

スカラー量は座標系が回転しても、その値は変わらない。このように回転に対して不変な 量をスカラー量と定義する。あるスカラー量$\phi$が与えられたとすると、この場合、座 標系を言う必要はない。空間のある点の温度は、座標系を回転させても変化しない。ベク トルの成分の場合、座標軸が異なるとそれは変化するのと大きな違いである。

2.4 内積(スカラー積)の定義

ベクトルの大きさの計算と全く同じようにして、ベクトル $\boldsymbol{A}$と $\boldsymbol{B}$の積、

$$\boldsymbol{A}\cdot\boldsymbol{B}=A_xB_x+A_yB_y+A_zB_z$$ (8)

もスカラー量であることが示される。この演算を内積の定義とする。この定義から、 $\boldsymbol{A}\cdot\boldsymbol{B}=\boldsymbol{B}\cdot\boldsymbol{A}$であることが直ちに分かる。

ここで、座標を回転させて、新しい $\mathrm{x}$軸 を $\boldsymbol{A}$の方向にすると、

$$A_x=\vert\boldsymbol{A}\vert A_y=0 A_z=0$$ (9)

$$B_x=\vert\boldsymbol{B}\vert\cos\theta B_y=\vert\boldsymbol{B}\vert\cos\zeta B_z=\vert\boldsymbol{B}\vert\cos\eta$$ (10)

となる。 $\theta, \zeta, \eta$はそれぞれの軸との方向余弦である。従って、内積の 定義より、

$$\boldsymbol{A}\cdot\boldsymbol{B}=\vert\boldsymbol{A}\vert\vert\boldsymbol{B}\vert\cos\theta$$ (11)

となる。$\theta$はベクトル $\boldsymbol{A}$と $\boldsymbol{B}$の間の角度と考える。これを内積の第二 の定義と考えることができる。実際には、式(8)と 式(11)の簡単な方を使えば良い。

本日、最初に示した位置エネルギーの変化 $\Delta U=\vert\boldsymbol{F}\vert\vert\boldsymbol{r}\vert\cos\theta$ は 内積の演算になっていることが分かる。

$$\Delta U=\boldsymbol{F}\cdot\boldsymbol{r}$$ (12)

そして、これはスカラー量となる。エネルギーはスカラー量なので当然の結果である。

最後に $\mathrm{x}, \mathrm{y}, \mathrm{z}$軸の単位ベクトル $\boldsymbol{i}, \boldsymbol{j}, \boldsymbol{k}$の内積の演算を示しておく。

$$\begin{aligned}&\boldsymbol{i}\cdot\boldsymbol{i}=1 & &\boldsym... ...mbol{j}=0 & &\boldsymbol{k}\cdot\boldsymbol{k}=1 \end{aligned}$$

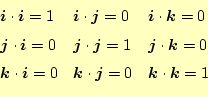[練習1]

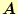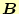2つのベクトル $\boldsymbol{A}$と $\boldsymbol{B}$の内積が、スカラー量で あることを示せ。

[練習2]

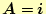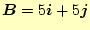内積の演算を利用して、ベクトル $\boldsymbol{A}=\boldsymbol{i}$と $\boldsymbol{B}=5\boldsymbol{i}+5\boldsymbol{j}$の間の角度を求めよ。

ホームページ: Yamamoto's laboratory
著者: 山本昌志