3 電磁波
ここでは、先ほどの電磁場の波動方程式のもっとも単純な解である平面波について、カー テシアン座標系で考察する。3.1 3次元平面波
先程述べたように、自由空間の電場を表す式(8)は波動方程式で、その解 は波になっている。波といってもベクトルである電場の波である。この解としてを仮定する。ここで、
![]() はベクトルで、
はベクトルで、
| (23) |
と成分で書き表すことができる。もちろん、
| (24) |
である。従って、式(24)中の
| (25) | |
| (26) | |
| (27) |
となる。これで、ベクトルの波を表す式(24)がわかった。
次に波数ベクトル
![]() の意味を考える。式(24)中の
の意味を考える。式(24)中の
![]() は、位相である。そこで、この位相一定が場所
は、位相である。そこで、この位相一定が場所
![]() 、
すなわち波面がどうなっているか考える。一定の位相を
、
すなわち波面がどうなっているか考える。一定の位相を![]() とすると、
とすると、
![]() なので、
なので、
| (28) |
となる。もちろん、波面はある瞬間の状態なので、同じは面の上では右辺は一定の値とな る。このことから、
もう少しこれを定量的に評価することにすることが良いだろう。![]() と
と
![]() 秒の
位相
秒の
位相![]() の波面の位置をそれぞれ、
の波面の位置をそれぞれ、
![]() と
と
![]() とすると
とすると
| (29) | ||
| (30) |
となる。この式の辺々を引くと
| (31) |
となる。この式の意味は、成分で書き表すと
| (32) |
となり、かなりわかりやすくなる。これから波面の速度は、
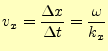 |
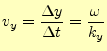 |
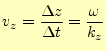 |
(33) |
と書き表すことができる。これは、波面の移動する速度で、位相速度と呼ばれる。これまでの話で、これが位相速度と呼ばれる理由がわかっただろう。成分で表された位相速度をベクトルで書き表すと、
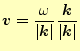 |
(34) |
となる。右辺の
これまでの話で、式(24)が3次元の平面波を表すことがわかった。
この平面波がマクスウェルの方程式から導かれた波動方程式(8)の解になっ
ているためには、パラメーターである角振動数![]() と波数
と波数
![]() はどのようになっ
ているだろうか?。それを調べるためには、式(24)を式
(8)の中に入れてみれば良い。すると、
はどのようになっ
ているだろうか?。それを調べるためには、式(24)を式
(8)の中に入れてみれば良い。すると、
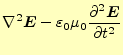 |
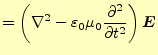 |
(35) |
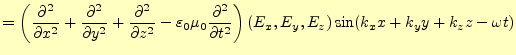 |
(36) | |
| (37) | ||
| (38) |
となる。任意の電場の大きさで、任意の場所で、いつでもこの式が成り立つためには、
| (39) |
とならなければならない。波数ベクトル
この式から直ちに波の速度の大きさが
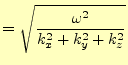 |
||
| (40) |
となることがわかる。これから、電磁波の速度は誘電率と透磁率から求めることができる。誘電率は
これは、光の速度と同じである。実は、光は電磁波なのである。これからは、光の速度を
![]() として、
として、
| (41) |
の記号を用いることにする。それにしても、磁石や静電気の現象が光と関係しているのは驚きである。
今までは、電場の平面波について論じて、式(24)が自由空間中のマクスウェルの方程式の解の一つになっていることを示した。同様に磁場の平面波も
マクスウェルの方程式の解になっているのは明らかである。
3.2 横波としての電磁波
3.2.1 波の進行方向と電場
次に、電場|
|
||
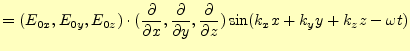 |
||
| (43) |
となる。これが、いつでもどこでも成り立つためには、
| (44) |
となる必要がある。これは、電場と平面波の進む方向が直交していると言っている。
3.2.2 波の進行方向と磁場
電場の波の式(24)と磁場の波の式(44)は全 く同じ形をしている。また、電場の発散の式(1)と磁 場の発散の式(2)も同じ形をしている。したがって、 磁場の場合も| (45) |
が成り立つ。やはり、磁場と平面波の進む方向は直交しているのである。
3.2.3 残りのマクスウェルの方程式
平面波について、マクスウェルの方程式の(1)と (2)が成立するためには、その進行方向と電場お よび磁場の方向が直交する必要があった。残りの方程式については、どうだろうか?。まずは、式(3)を考える。この式の左辺は
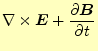 |
![$\displaystyle =\nabla\times \left[\boldsymbol{E}_0\sin(\boldsymbol{k}\cdot\bold...
...i \left[\boldsymbol{B}_0\sin(\boldsymbol{k}\cdot\boldsymbol{r}-\omega t)\right]$](img138.png) |
|
| ベクトル恒等式、
|
||
![$\displaystyle =\nabla\times \left[\boldsymbol{E}_0\sin(\boldsymbol{k}\cdot\bold...
...i \left[\boldsymbol{B}_0\sin(\boldsymbol{k}\cdot\boldsymbol{r}-\omega t)\right]$](img140.png) |
||
| |
||
| (46) |
となる。これがいつでも、どこでも成り立つためには、
となる必要がある。この式から、電場と磁場、波の進む方向と磁場は直交している ことが分かる。
これまでの全ての議論から、
電場と磁場、波の進む方向は全て直交している。
ということがわかった。
残りは、マクスウェルの方程式の(4)である。この式を計算
しやすくするために、
![]() を使って
を使って
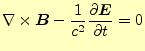 |
(48) |
と書き直しておく。この式は(4)とほとんど同じなので、電 場や磁場の波の式を代入した結果は、
| (49) |
と直ちにわかる。これが、いつでもどこでも成り立つためには
である。やはり、電場と磁場、電場と波の方向は直交している。
これまでのところ、電場と磁場、波の進む方向がおのおの直交しいれば、波の方程式 (24)と(44)は同時に成り立つことが分かっ た。条件は、それだけでよいのだろうか?。まだだめである。式 (49)と式(52)が連立して成立する必要があ る。これは、
| (51) | ||
| (52) |
と書き改められる。電場
| (53) | ||
| (54) |
と容易に導くことができる。これから、直ちに
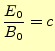 |
(55) |
となる。真空中の電磁波は、電場と磁場の比がいつも一定なのである。
この式から、
![]() の関係をつかって、
の関係をつかって、
| (56) |
と言う式が導かれる。技術者はこの関係を憶えている。この376.7
3.3 電磁波のエネルギー
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月24日
![\includegraphics[keepaspectratio, scale=1.0]{figure/hamen.eps}](img102.png)