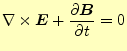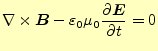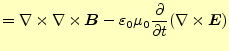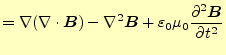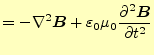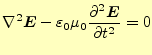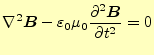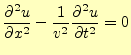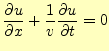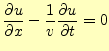2 自由空間内の電磁波の波動方程式
2.1 電磁場の波動方程式
この講義の最初に、遠隔作用と近接作用(場の採用)の考え方を示した。そのときに、遠隔 作用の考え方が困難をきたす場合として、電波の話をした。いよいよその電波の話をする 事になる。静電場の場合、遠隔作用であろうが近接作用であろうがその現象は変わらなかった。ただ、 近接作用、すなわち場の考え方を採用した方が計算は容易であったことは確かであるが、 物理現象は同じように説明できた。電磁場の振動の周波数が高くなると、その考えは出来 なくなる。それは、どのだろうか?。それについては、最後に述べることにしよう。
最初に、真空で電荷や電流が存在しない自由空間の電磁場を考える。電荷や電流が存在し ない空間だから、電場や磁場もゼロと考えるかもしれない。今までの話だと、電場や磁場 の源は、電荷や電流と言ってきたので、そう思っても仕方がない。実際にどうなっている か、マクスウェルの方程式から考えることにしよう。自由空間でそれは、
となる。明らかに、
この方程式を直接計算することは、明らかに計算が大変である。ベクトルの連立偏微分方 程式になっているからである。ベクトルの部分は成分に分ければスカラーの方程式にする 事ができる。問題なのは電場と磁場の連立になっているからである。電場あるいは磁場の 単独の式にする必要がある。自由空間のマクスウェルの方程式を眺めると分かるが、式 (3)の両辺の回転を取ると
| 0 | 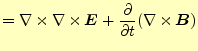 |
|
| 式(4)より | ||
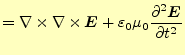 |
(5) |
となり、電場のみの式にできる。ここで、右辺第一項であるが、これはベクトル恒等式
| 0 | 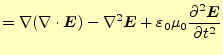 |
|
| 式(1)より | ||
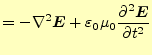 |
(6) |
と変形できる。これで、電場のみの式となった。
同じことを磁場に適用する。式(4)の両辺の回転をとること から始めると、
が得られる。
以上の操作により、自由空間中での電場と磁場を表す2組の方程式
が得られた。この方程式は、物理的には何を意味しているのだろうか?。以前の講義で話 したように、カーテシアン座標系のラプラス演算子は、
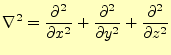 |
(9) |
となる。また、電場
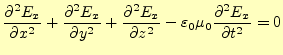 |
(10) |
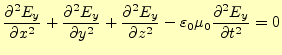 |
(11) |
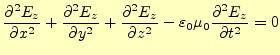 |
(12) |
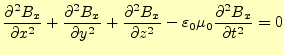 |
(13) |
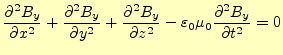 |
(14) |
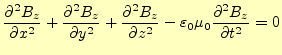 |
(15) |
と書き改められる。このように6組の偏微分方程式が得られる。
この方程式は、どこかで見覚えがあるはずである。波動方程式である。電磁場の波動方程 式となっている。このようになると、近接作用の考えが生きてくる。遠隔作用の考えでは 波動方程式などでてこないのである。さて、この近接作用が確固たるものになるためには 電磁場の波を観測しなくてはならない。それが、1888年にヘルツによって観測されたので ある。物理学上のもっともドラマチックな実験に違いない。理論から予言された電磁波が 本当にあったのである。この電磁波の発見は、その後の科学技術に多大な貢献をした。そ の内容は言うまでもないだろう。
古代の磁石や静電気の研究から始まり、エルステッドやクーロン、アンペール、ファラ デー、その他多くの人の研究は、マクスウェルの方程式となり、最後のヘルツが決定的な 実験をして、電磁気学は完成したのである。最後に、よちよち歩きの赤ちゃんは、現代社 会の繁栄をもたらす巨大な技術として成長したのである。
2.2 波動方程式(復習)
たぶん、諸君が最初に学習した波動方程式は、1次元でのようになっていたはずである。
波は重ね合わせの原理が成り立つことはよく知られた事実である。だから、遠くまでの通
信ができるのである。![]() と
と![]() が式(17)が解ならば、
任意定数
が式(17)が解ならば、
任意定数![]() と
と![]() をつかって
をつかって
| (17) |
も解となることが重ね合わせの原理である。この新しい関数
それでは、波動方程式の一般解を求めることにしよう。式(17)は
| 0 | 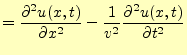 |
|
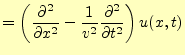 |
||
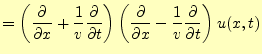 |
と書き換えることができるので、
ならば、元の波動方程式の解となる。最初の偏微分方程式の解は、
| (19) |
となることが分かる。本当かどうかは、これを元の式(20)の最初 に代入してみればよい。明らかに成り立つはずである。同様に、2番目の偏微分方程式の 解は、
| (20) |
となることがわかる。最初の
最初に述べたように波動方程式の解は重ね合わせの原理が成り立つ。したがって、先ほど の2つの解は結合されて
| (21) |
と書き表すことができる。要するに、波動方程式の解は進行波と後進波の和になるのであ る。もし、
ここでは、波動方程式の解としてダランベールの解を示した。しかし、諸君は4年生の応 用解析では、式(17)を変数分離して解いたはずである。変数分離で解 いたものがダランベールの解になっていることを確認してみるとよい。また、電気の学生 は5年生の計算機応用で、波動方程式を差分で計算したはずである。このように様々な方 法で、波動方程式は解くことができる。問題に適した方法で計算できるようになる必要が ある。なぜならば、波動方程式は自然科学の分野でかなりポピュラーで、しばしば現れる からである。
風呂に入っているとき、水面を静かにして、水滴を一滴落とし、波面が広がる様子をとき どき観察する。落下した水滴により、孤立波が発生し、それが静かに円形に広がり、壁に 衝突する。壁に衝突した反射波もまた円形に広がる。私は、このように波がきれいに広が ることが信じられず、大きな感動を覚えるのである。流体のように粘性が支配するような 媒質でも、あのようにきれいに波が広がることは私にはまったく信じられない。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月24日