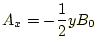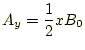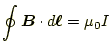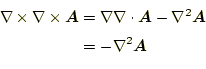静電場のときに話したポテンシャル2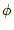 は、
は、
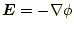 |
(1) |
と決めた。これは、
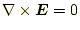 が成り立つため、スカラー場
が成り立つため、スカラー場
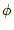 を使うことができた。今までの学習してきた言葉で言えば、電圧の変化
の割合が電場である。このポテンシャルは、位置
を使うことができた。今までの学習してきた言葉で言えば、電圧の変化
の割合が電場である。このポテンシャルは、位置
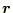 のみの関数で、座標
が決まれば、値が決まる。これは、山の高さみたいなもので、地図の上で経度
(x座標)と緯度(y座標)を決めれば山の高さ(
のみの関数で、座標
が決まれば、値が決まる。これは、山の高さみたいなもので、地図の上で経度
(x座標)と緯度(y座標)を決めれば山の高さ(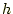 )が求まるのと同じである。そ
の山の勾配が
)が求まるのと同じである。そ
の山の勾配が
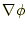 である。
である。
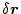 移動したときの、山の高さ
の変化
移動したときの、山の高さ
の変化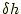 は
は
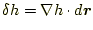 |
(2) |
と書けるだろう。したがって、微分の規則から、勾配の演算は
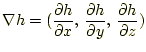 |
(3) |
となる。
山の中をうろうろして、元の場所に戻ると、その位置エネルギー3(mgh)の変化
はない。これは、山の高さ(ポテンシャル)、あるいは位置エネルギーが座標
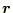 のみの関数であるからである。このような場から、導かれる場を保存
力と言う。万有引力、重力、弾性力、静電力などがその例である。ポテンシャ
ルエネルギーを
のみの関数であるからである。このような場から、導かれる場を保存
力と言う。万有引力、重力、弾性力、静電力などがその例である。ポテンシャ
ルエネルギーを
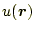 とすると、保存力
とすると、保存力
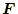 とは
とは
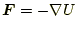 |
(4) |
の関係がある。そして、物体が点
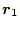 から
から
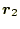 に移動する場合、
この保存力がする仕事は、
に移動する場合、
この保存力がする仕事は、
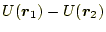 となる。途中の道筋に
よらない。
となる。途中の道筋に
よらない。
静電場の多くの問題は、電荷密度が与えれている場合、電場分布を求めること
になる。この場合、このポテンシャルは非常に便利である。通常の問題であれ
ば、直接電場を求めるよりは、ポテンシャルを求めてから、それの勾配を計算
することにより電場を導くのが簡単である。具体的には、ポアッソン方程式
を解くか、その解である
の積分を計算するかである。問題に応じて、使い分ければよい。
静電場の場合、ポテンシャルの考え方は非常に強力である。同じようなテクニッ
クが静磁場の計算に使えれば便利である。静電場の場合、
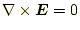 と式から、スカラーポテンシャル
と式から、スカラーポテンシャル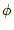 と言うものを
使うことにした。不幸なことに、静磁場の場合
と言うものを
使うことにした。不幸なことに、静磁場の場合
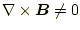 な
ので、静電場のようにはいかない。静磁場の場合、
な
ので、静電場のようにはいかない。静磁場の場合、
を使うことになる。発散がゼロなので、
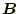 は何かの回転と書くことができる。
要するに、
は何かの回転と書くことができる。
要するに、
である。これを、式(7)に代入すると、
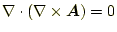 で、確かに良い。この
で、確かに良い。この
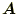 をベク
トルポテンシャルと言う。
をベク
トルポテンシャルと言う。
スカラーポテンシャルの場合、それに任意の定数を加えても、静電場は変わら
なかった。そこで、計算が便利なように、
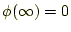 と基準ポテンシャ
ル(基準電位)を決めた。ベクトルポテンシャルも、任意の定数を加えても、そ
れが表現する磁場を同じである。ベクトルポテンシャルの場合、さらに任意性
があり、任意のスカラー場
と基準ポテンシャ
ル(基準電位)を決めた。ベクトルポテンシャルも、任意の定数を加えても、そ
れが表現する磁場を同じである。ベクトルポテンシャルの場合、さらに任意性
があり、任意のスカラー場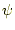 の勾配を加えても、それが表現する磁場は同
じである。すなわち、
の勾配を加えても、それが表現する磁場は同
じである。すなわち、
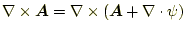 |
(9) |
である。
このような場合、計算の都合の良いようにある条件を課して、パラメーターの
自由度を減らしておくと良い。スカラーポテンシャルの場合、無限遠点で、値
をゼロに決めたようにである。静磁場の計算では、
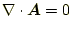 |
(10) |
とするのが都合が良い。これを、クーロンゲージと言う。なぜこれが都合が良
いかは後でわかる。ところで、磁場を変えないで、この条件を満たすことがで
きるのだろうか?。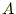 に任意のスカラー場の勾配を加えることが可能であるこ
とは、先に述べたとおりである。それでは、
に任意のスカラー場の勾配を加えることが可能であるこ
とは、先に述べたとおりである。それでは、
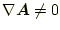 である
である
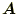 に任意のスカラー場を加えて、発散を計算してみる。これは、
に任意のスカラー場を加えて、発散を計算してみる。これは、
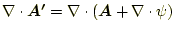 |
(11) |
となる。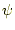 は任意に選ぶことができるから、
は任意に選ぶことができるから、
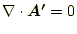 |
(12) |
とすることができる。なんとなく良いように思えるが、本当かなー、よくわか
らん。実際は、良いのであるが、ほかの方法を考える。
もう少し元に戻って、ベクトルポテンシャル
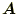 は、式
(8)を満足すればよいだけである。
は、式
(8)を満足すればよいだけである。
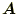 を決めるためには、そ
の発散を決めればよい。その発散は、どんな値をもとりうる。したがって、
を決めるためには、そ
の発散を決めればよい。その発散は、どんな値をもとりうる。したがって、
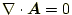 としても良いはずである。以上のことをまとめると、
ベクトルポテンシャルは
としても良いはずである。以上のことをまとめると、
ベクトルポテンシャルは
の2つの方程式から決めることができる。
実際、ベクトルポテンシャルはどのような形をしているか、考えよう。この辺
は、「ファインマン物理学 III 電磁気学」を参考にしている。
z方向に一様な磁場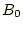 の場合を考える。ベクトルポテンシャルの定義より、
の場合を考える。ベクトルポテンシャルの定義より、
\begin{align*}
&B_x=\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z}=0\\
&B_y=\frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x}=0\\
&B_z=\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}=B_0\\
\end{align*}
となる。この式から、可能な解は、
がある。この解は明らかに、
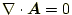 である。同じように、も
うひとつ、
である。同じように、も
うひとつ、
の解があることも直ちに解る。これも、発散はゼロである。また、これらの解
を組み合わせて
という解もできる。いずれにしても、いろいろなベクトルポテンシャルがあり、
どれも同じ磁場を表す。
以前の授業で、ベクトル場の発散と回転が決まれば、そのベクトル場は一意に
決まるといった。それにもかかわらず、ここでは少なくとも3つのベクトルポ
テンシャルが可能なのはなぜか?。よく考えてみよう。
先週の授業でやったアンペールの法則
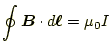 |
(19) |
の微分形は
である。これらは、ストークスの定理で結ばれていることを十分理解する必要
がある。この微分形を用いて、電流密度分布
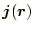 が作るベクトル
ポテンシャルを計算する。これは、電荷分布
が作るベクトル
ポテンシャルを計算する。これは、電荷分布
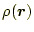 がスカラーポテン
シャルを作ったのと同じである。
がスカラーポテン
シャルを作ったのと同じである。
式(20)にベクトルポテンシャルを代入すると、
なので、
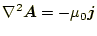 |
(22) |
となる。これは、ベクトルの微分方程式である。それぞれの成分は、
となる。
これは、静電場の場合のスカラーポテンシャルの式
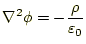 |
(24) |
とそっくりではないか。この方程式の解、つまり図1の
点Pでのポテンシャルは
となることは以前に学習したとおりである。ベクトルポテンシャルの各成分の
式はスカラーポテンシャルとまったく同じ形をしているので、解も同じ形であ
る。各成分で書き表すのは面倒くさいので、ベクトルで書くと
となる。電流分布が与えられたとき、この積分を行い、その結果の回転を計算
することにより磁場を求めることができる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成16年10月23日
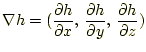
![]() のみの関数であるからである。このような場から、導かれる場を保存
力と言う。万有引力、重力、弾性力、静電力などがその例である。ポテンシャ
ルエネルギーを
のみの関数であるからである。このような場から、導かれる場を保存
力と言う。万有引力、重力、弾性力、静電力などがその例である。ポテンシャ
ルエネルギーを
![]() とすると、保存力
とすると、保存力
![]() とは
とは
![]() と基準ポテンシャ
ル(基準電位)を決めた。ベクトルポテンシャルも、任意の定数を加えても、そ
れが表現する磁場を同じである。ベクトルポテンシャルの場合、さらに任意性
があり、任意のスカラー場
と基準ポテンシャ
ル(基準電位)を決めた。ベクトルポテンシャルも、任意の定数を加えても、そ
れが表現する磁場を同じである。ベクトルポテンシャルの場合、さらに任意性
があり、任意のスカラー場![]() の勾配を加えても、それが表現する磁場は同
じである。すなわち、
の勾配を加えても、それが表現する磁場は同
じである。すなわち、
![]() は、式
(8)を満足すればよいだけである。
は、式
(8)を満足すればよいだけである。
![]() を決めるためには、そ
の発散を決めればよい。その発散は、どんな値をもとりうる。したがって、
を決めるためには、そ
の発散を決めればよい。その発散は、どんな値をもとりうる。したがって、
![]() としても良いはずである。以上のことをまとめると、
ベクトルポテンシャルは
としても良いはずである。以上のことをまとめると、
ベクトルポテンシャルは
![]() の場合を考える。ベクトルポテンシャルの定義より、
の場合を考える。ベクトルポテンシャルの定義より、