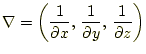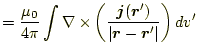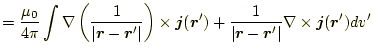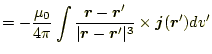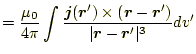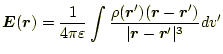2 ビオ-サバールの法則

次に、式(26)の回転を計算することにより、磁 場を求めてみる。当然、点Pの回転を求めるため、演算子は

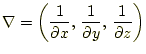$$\nabla=\left(\frac{1}{\partial x},\, \frac{1}{\partial y},\, \frac{1}{\partial z}\right)$$ (27)

となる。 $\boldsymbol{r}^\prime$での微分ではない。

ベクトル解析の恒等式

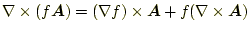$$\nabla\times(f\boldsymbol{A})=(\nabla f)\times\boldsymbol{A}+f(\nabla\times\boldsymbol{A})$$ (28)

と、

$$\nabla\left(\frac{1}{\vert\boldsymbol{r}-\boldsymbol{r}^\prime\ve... ...bol{r}-\boldsymbol{r}^\prime}{\vert\boldsymbol{r}-\boldsymbol{r}^\prime\vert^3}$$ (29)

に注意して、計算を進める。

磁場は、式(26)の回転を計算することにより、

$$\boldsymbol{B}(\boldsymbol{r}) =\nabla\times\boldsymbol{A}$$

$$% =\frac{\mu_0}{4\pi} \int\nabla\times\left(\frac{ \boldsymbol{j}(\... ...bol{r}^\prime)}{\vert\boldsymbol{r}-\boldsymbol{r}^\prime\vert}\right)dv^\prime$$

$$% =\frac{\mu_0}{4\pi}\int\nabla\left( \frac{1}{\vert\boldsymbol{r}-... ...bol{r}^\prime\vert} \nabla\times\boldsymbol{j}(\boldsymbol{r}^\prime) dv^\prime$$

$$% \nabla\times\boldsymbol{j}(\boldsymbol{r}^\prime)=0$$

$$% =-\frac{\mu_0}{4\pi}\int \frac{\boldsymbol{r}-\boldsymbol{r}^\pri... ...dsymbol{r}^\prime\vert^3} \times\boldsymbol{j}(\boldsymbol{r}^\prime) dv^\prime$$

$$% =\frac{\mu_0}{4\pi}\int \frac{\boldsymbol{j}(\boldsymbol{r}^\prim... ...symbol{r}^\prime)} {\vert\boldsymbol{r}-\boldsymbol{r}^\prime\vert^3} dv^\prime$$ (30)

となる。この電流と磁場の関係を「ビオ-サバールの法則」と言う。これは、 静電場を求める式

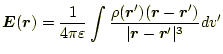$$\boldsymbol{E}(\boldsymbol{r})=\frac{1}{4\pi\varepsilon}\int \fra... ...symbol{r}^\prime)} {\vert\boldsymbol{r}-\boldsymbol{r}^\prime\vert^3} dv^\prime$$ (31)

と同じ形であることに注意してほしい。

「ビオ-サバールの法則」についての、残りの説明は、教科書の通り。

ホームページ: Yamamoto's laboratory
著者: 山本昌志