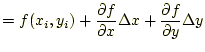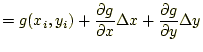2 非線型連立方程式の実数解(2元の場合)
2.1 非線型連立方程式とは
今まで、諸君は、「非線型の方程式」あるいは「線形の連立方程式」は解いた ことがある。例えば、前者は、| (1) |
のようなものである。後者の例は、
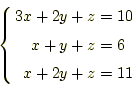 |
である。非線型方程式は未知数が2次以上のものをいい、連立方程式 は未知数が2個以上のものをいうのである。非線型とは、直線でないという意 味である。未知数が2次以上のもの、例えば
非線型なn次方程式は、複素数解を考えると、n個の解がある。線形な連立方程 式、n元1次方程式の場、合係数が特異でない限り、1個の解がある。では、非 線形な連立方程式、n元m次方程式の場合、複素数を含めた解の数はm個のよう に思えるが、正しいのだろうか?。数学の先生に聞くと、正しいということで ある。
また、方程式の数と未知数の数は一致しなくてはならないのは、通常の連立方 程式と同じである。それらの数が同じでも、線形連立方程式では、係数行列の 行列式がゼロの場合、解は一意に決まらない。非線型の連立方程式の場合、こ れはどのような場合に対応するのだろうか?。私には、分からない。かなり難 しく興味深い問題のように思えるが、ここではそのことは考えないことにする。
2.2 非線型連立方程式の例
実例を使って、計算方法を示す。例として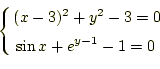 |
の近似解を求めることを考える。2元?次非線型連立方程式である。?次とは、 いささかいい加減に書いているが、勘弁してもらいたい。無限次といってよい ような気がするが自信が無いので?マークを付けておく。
さて、この方程式の解であるが、それをグラフに示す。2元であればグラフに
書くことができるのである。以下の議論は、任意の元の方程式でも成り立つこ
とは理解して欲しい。これらの方程式をグラフに書くと図
![[*]](crossref.png) のようになる。図中に示すように、点AとBに実数解があ
るのが分かるであろう。
のようになる。図中に示すように、点AとBに実数解があ
るのが分かるであろう。
初期値から出発して、解であるAやB点に近づく方法を考える。そこで、次のよ うな関数を考える。
| (4) | ||
| (5) |
もちろん、
いつものように、この非線型連立方程式の解を
![]() とする。
当然、
とする。
当然、
![]() かつ
かつ
![]() である。そ
して、
である。そ
して、![]() 番目の近似解を
番目の近似解を
![]() とする。ここから、
とする。ここから、
![]() だけ移動したところの値は、
だけ移動したところの値は、
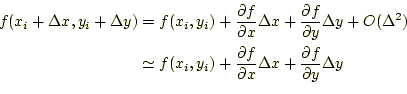 |
となる。
となる。
ここで、
![]() かつ
かつ
![]() となるように、
となるように、![]() と
と![]() を選ぶとする。このようにする
ためには、
を選ぶとする。このようにする
ためには、![]() と
と![]() はつぎの連立方程式を満たせばよい。式
(7)と(8)の左辺をゼロとおき式を
整理すれば
はつぎの連立方程式を満たせばよい。式
(7)と(8)の左辺をゼロとおき式を
整理すれば
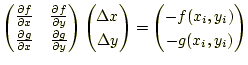 |
(9) |
となる。この連立方程式を解いて、
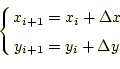 |
となる。これが、非線型連立方程式の漸化式である。
2.3 連立で無い場合とのアナロジー
以前の授業で示した方程式の実数解や複素数解を求めたのと同じようなことを、 ここでも行った。式も似ているし、考え方も同じである。以前は、- 解に近いところでは、直線で近似できる2。
- 解に近いところでは、平面で近似できる3。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年9月13日
![\includegraphics[keepaspectratio, scale=1.0]{figure/ZeroPoint.eps}](img7.png)