3 非線型連立方程式の解(多元の場合)
前章では、2元の非線型連立方程式のニュートン法での計算方法を示した。こ こでは、それを一般化する。ここで示す方法は、複素数解にも適用できる。N元の非線型連立方程式は、
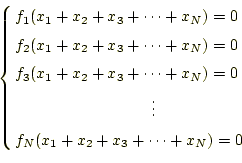 |
と書くことができる。未知数は、
| (12) |
とベクトルで表現する。すると、
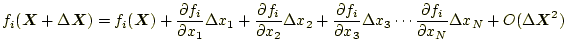 |
(13) |
となる。
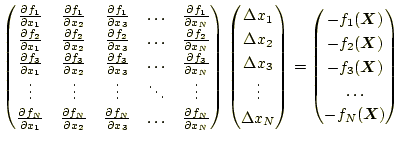 |
(14) |
の線形であるN元1次連立方程式が成り立つ。これを解いて、
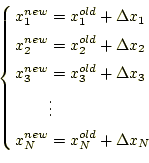 |
となる
非線型の連立方程式を線形の連立方程式で計算しているわけである。解きやす
い式になった分、反復計算が必要となっている。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年9月13日