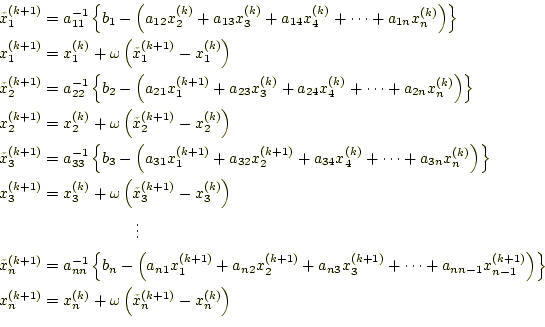6 SOR法

ここでは、より高速な逐次加速緩和法(SOR法:Successive Over-Relaxation)について説明 する。このでの説明は、文献 [2]を参考にした。この教科書 には、行列の計算テクニックが多く欠かれているので便利で、このような計算をする人は 参考書として持っておくのが良いだろう。

ガウス・ザイデル法をもっと改善する方法がある。ガウス・ザイデル法の解の修正は、 $x_{k+1}-x_k$であったが、これをもっと大きなステップにしようというのである。通常 の場合、ガウス・ザイデル法では近似解はいつも同じ側にあり、単調に収束する。そのた め、修正を適当にすれば、もっと早く解に近づく。修正幅を、加速緩和乗数$\omega$を用 いて、 $\omega(x_{k+1}-x_k)$とする事が考えられた。これが、SOR法である。

具体的な計算手順は、次のようにする。ここでは、ガウス・ザイデル法の式 (26)を用いて、得られた近似解を $\tilde{x}_i^{(k+1)}$としている。

$$\begin{aligned}&\tilde{x}_1^{(k+1)}=a_{11}^{-1}\left\{b_1-\left... ...mega\left(\tilde{x}_n^{(k+1)}-x_n^{(k)}\right)\\ % \end{aligned}$$

これが、SOR法である。

ここで、問題なのが加速緩和係数$\omega$の値の選び方である。明らかに、それが1の場 合、ガウス・ザイデル法となりメリットは無い。また、1以下だと、ガウス・ザイデル法 よりも収束が遅い。ただし、ガウス・ザイデル法で収束しないような問題には使える。

従って、1以上の値にしたいわけであるが、余り大きくすると、発散するのは目に見えて いる。これについては、2を越えると発散することが分かっている。最適値となると、だ いたい1.9くらいが選ばれることが多い。

ホームページ: Yamamoto's laboratory
著者: 山本昌志