常微分方程式を数値計算で解く方法として、もっとも単純ですが、最も精度の
悪い方法です。よっぽどのことが無い限り、この方法で微分方程式を計算して
はいけません。ただし、常微分方程式を数値計算することのイメージはつかみ
やすいでで述べておきます。
もう一度、初期条件を含めて数値計算により解くべき方程式を示します。
この微分方程式の解を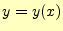 とすると、
とすると、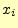 のまわりのテイラー展開は、
のまわりのテイラー展開は、
です。この式の右辺第2項は、式(6)
から計算できます。したがって、テイラー展開は、次のように書き表すことが
出来ます。
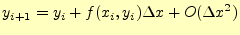 |
(8) |
オイラー法での数値計算では、計算の刻み幅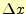 は十分に小さいとして、
は十分に小さいとして、
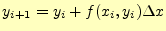 |
(9) |
を計算します。式(5)と全く同じです。このとき計算の精
度は1次と言います2。
オイラー法をまとめると、以下に示すように微分方程式は差分方程式に変換さ
れます。
オイラー法での数値計算は、次の漸化式に従い計算します。解である
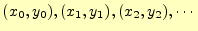 が同じ手続きで計算できます。
実際にプログラムを行うときは、forやwhileを用いて繰り
返し計算を行い、結果の
が同じ手続きで計算できます。
実際にプログラムを行うときは、forやwhileを用いて繰り
返し計算を行い、結果の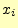 と
と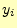 は、配列x[i] や
y[i]に格納します。
は、配列x[i] や
y[i]に格納します。
この方法の計算のイメージは、図4の通りです。明らか
に、出発点の導関数のみ利用しているために精度が悪いことが分かります。式
も対称でないため、逆から計算すると元に戻りません。
図 4:
オイラー法。ある区間での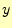 の変化
の変化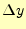 は、計算の始めの
点の傾きに区間の幅
は、計算の始めの
点の傾きに区間の幅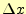 を乗じて、求めている。
を乗じて、求めている。
|
|
2次のルンゲ・クッタと呼ばれる方法は、いろいろあります。ここでは、教科
書に載っているホイン法と中点法を示します。オイラーは1次の精度でしたが、
これらは2次の精度があります。
先に示したように、オイラー法の精度は1次です。それに対して、2次のルンゲ・
クッタ法の精度は2次です。教科書に書いてある方法で公式を導き出し、その
精度を示します。今まで刻み幅を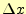 と記述していましたが、教科書に
合わせて
と記述していましたが、教科書に
合わせて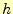 と表現します。
と表現します。
2次の精度ということは、テイラー展開より
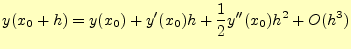 |
(12) |
となっていることを意味します。即ち、計算アルゴリズムが、
となっていることを言います。最終目標が分かったので、教科書と同じ方法で
計算公式を導きましょう。
式(13)から分かるように、 の増分
の増分 を計算する
ためには、1階微分と2階微分の2項を満たす式が必要です。そうすると少なく
とも、2点の値が必要となります。2点として、計算区間の両端の導関数の値を
使います。この導関数は問題として与えられているので、計算は簡単です。そ
うして、区間の増分を
を計算する
ためには、1階微分と2階微分の2項を満たす式が必要です。そうすると少なく
とも、2点の値が必要となります。2点として、計算区間の両端の導関数の値を
使います。この導関数は問題として与えられているので、計算は簡単です。そ
うして、区間の増分を
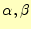 をパラメーターとした和で表すことに
します。即ち、以下の通りです。
をパラメーターとした和で表すことに
します。即ち、以下の通りです。
この
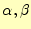 を上手に選ぶことにより、式(13)と同
一にできます。この式を
を上手に選ぶことにより、式(13)と同
一にできます。この式を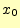 の回りでテイラー展開すると
の回りでテイラー展開すると
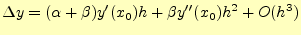 |
(15) |
となります。これを、式(13)と比較すると、
とすれば良いことが分かります。これで、必要な式は求まりました。まとめる
と、式(6)を数値計算で近似解を求める
には次式を使うことになります。
この式は、図5のようになります。オイラー法の図
4との比較でも、精度が良いことが分かります。
図 5:
ホイン法(教科書の方法)。ある区間での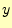 の変化
の変化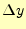 は、
計算の始めと終わりの点付近の平均傾きに区間の幅
は、
計算の始めと終わりの点付近の平均傾きに区間の幅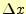 を乗じて、求
めている。
を乗じて、求
めている。
|
|
よく見ると、この式(17)は、本当に2次の精度があるのでしょう
か?。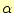 や
や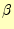 のパラメーターを計算したときの
のパラメーターを計算したときの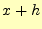 の導関数は
の導関数は
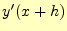 を使いました。一方、式(17)では、
を使いました。一方、式(17)では、
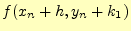 を使っています。ほんのちょっと違いますので、式
(17)が2次の精度を持っているか、検証してみましょう。この式を
変形することで、精度を確認しましょう。紙面の都合上、精度の確認は2段階
で行います。まず初めは、少なくとも2次の精度があることを確認します。そ
の後、3次の精度はないことを示します。
を使っています。ほんのちょっと違いますので、式
(17)が2次の精度を持っているか、検証してみましょう。この式を
変形することで、精度を確認しましょう。紙面の都合上、精度の確認は2段階
で行います。まず初めは、少なくとも2次の精度があることを確認します。そ
の後、3次の精度はないことを示します。
この結果は、まさに式(7)と同じ形をしており、少なくとも
2次の精度があることが確認できます。式(18)を変形
するときに、次式を用いたので注意が必要です。
次に3次の精度がないことを示します。テイラー展開の3次の項は、係数は無視
すると、
となります。一方、ホイン法の2次公式の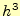 の項、即ち式(
の項、即ち式(![[*]](crossref.png) )の右辺のテイラー展開の2次の項は、以下の通りです。
)の右辺のテイラー展開の2次の項は、以下の通りです。
明らかに、テイラー展開の3次の項である式(![[*]](crossref.png) )とホイン法の3次の項の式(21)は異なってい
ます。したがって、ホイン法は3次の精度がないことが分かります。少なくと
も2次の精度があって、3次の精度がないことが示され、ホイン法は2次の精度
であることが証明されました。
これも、ホイン法と同じ2次の精度です。ホイン法は区間の両端の点の導関数
を使いましたが、中点方は始点と中点を使います。2点ありますので2次の精度
になります。ホイン法の式(14)に対応するものは、
)とホイン法の3次の項の式(21)は異なってい
ます。したがって、ホイン法は3次の精度がないことが分かります。少なくと
も2次の精度があって、3次の精度がないことが示され、ホイン法は2次の精度
であることが証明されました。
これも、ホイン法と同じ2次の精度です。ホイン法は区間の両端の点の導関数
を使いましたが、中点方は始点と中点を使います。2点ありますので2次の精度
になります。ホイン法の式(14)に対応するものは、
となります。これを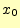 の回りでテイラー展開すると、
の回りでテイラー展開すると、
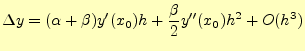 |
(23) |
となります。これを、式(13)と比較すると、
となります。したがって、中点法の公式は、
となります。この公式は、図6のようになります。これが2次の
精度であることの証明は、式(18)と同じ手順で、以下の
通りです。
これで少なくとも2次の精度があることが分かります。一方、3次の精度がない
ことは、以下の通り明らかである。式(21)と比べ
て、微小変位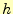 は、
は、
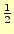 異なるだけですので、計算結果は、
と直ちに分かります。
異なるだけですので、計算結果は、
と直ちに分かります。
これもまた、式(20)と異なりますので、3次
の精度がないことが分かります。
図 6:
中点法。ある区間での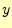 の変化
の変化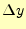 は、中点付近の傾きに
区間の幅
は、中点付近の傾きに
区間の幅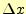 を乗じて、求めている。
を乗じて、求めている。
|
|
今まで示したオイラー法や2次のルンゲ・クッタ法のように、パラメーターを
増やして誤差項の次数を上げていく方法で、最良の方法と言われるのが4次の
ルンゲ・クッタ法です。パラメーターを増やして、5, 6, 7,  と誤差
項を小さくすることは可能ですが、同じ計算量であれば4次のルンゲ・クッタ
の刻み幅を小さくするほうが精度が良いです。私は、5次以上のルンゲ・クッ
タの公式は見たことがありません。
と誤差
項を小さくすることは可能ですが、同じ計算量であれば4次のルンゲ・クッタ
の刻み幅を小さくするほうが精度が良いです。私は、5次以上のルンゲ・クッ
タの公式は見たことがありません。
ということで、皆さんが常微分方程式を計算する必要が生じたときは、何はと
もあれ4次のルンゲ・クッタで計算してください。「この問題を解く場合、4次
のルンゲクッタだな」と一言いって、プログラムを書き始めると、出来るなと
思われること間違いなしです。間違っても「2次のルンゲ・クッタ 」
と言ってはいけません。「4次の方が
」
と言ってはいけません。「4次の方が 」と言う輩が出てきます。普通
の科学に携わる人にとって、4次のルンゲ・クッタは常微分方程式の最初で最
後の解法なのです。
」と言う輩が出てきます。普通
の科学に携わる人にとって、4次のルンゲ・クッタは常微分方程式の最初で最
後の解法なのです。
ただし、4次のルンゲ・クッタ法よりも精度の良い方法がないわけでは有りま
せん。より高精度な方法として、Bulirsch-Store法や予測子・修正法などがあ
ります。進んだ勉強をしたいときに、学習してください。
4次のルンゲ・クッタの公式は、式(28)に示す通りです。そし
て、これは図7のように表せます。
2次の場合と同じ手順で、公式を導き、そして4次の精度であることが証明でき
ると思います。しかし、計算は明らかに大変なので、腕力のある人はトライし
てみてください。
図 7:
4次のルンゲ・クッタ法。ある区間での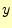 の変化
の変化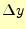 は、区
間内の4点の傾きのある種の加重平均に幅
は、区
間内の4点の傾きのある種の加重平均に幅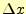 を乗じて、求めている。
を乗じて、求めている。
|
|
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年8月21日
![]() は十分に小さいとして、
は十分に小さいとして、
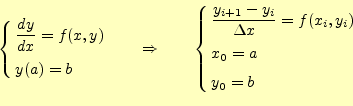
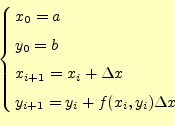
![]() の増分
の増分![]() を計算する
ためには、1階微分と2階微分の2項を満たす式が必要です。そうすると少なく
とも、2点の値が必要となります。2点として、計算区間の両端の導関数の値を
使います。この導関数は問題として与えられているので、計算は簡単です。そ
うして、区間の増分を
を計算する
ためには、1階微分と2階微分の2項を満たす式が必要です。そうすると少なく
とも、2点の値が必要となります。2点として、計算区間の両端の導関数の値を
使います。この導関数は問題として与えられているので、計算は簡単です。そ
うして、区間の増分を
![]() をパラメーターとした和で表すことに
します。即ち、以下の通りです。
をパラメーターとした和で表すことに
します。即ち、以下の通りです。
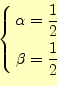
![]() や
や![]() のパラメーターを計算したときの
のパラメーターを計算したときの![]() の導関数は
の導関数は
![]() を使いました。一方、式(17)では、
を使いました。一方、式(17)では、
![]() を使っています。ほんのちょっと違いますので、式
(17)が2次の精度を持っているか、検証してみましょう。この式を
変形することで、精度を確認しましょう。紙面の都合上、精度の確認は2段階
で行います。まず初めは、少なくとも2次の精度があることを確認します。そ
の後、3次の精度はないことを示します。
を使っています。ほんのちょっと違いますので、式
(17)が2次の精度を持っているか、検証してみましょう。この式を
変形することで、精度を確認しましょう。紙面の都合上、精度の確認は2段階
で行います。まず初めは、少なくとも2次の精度があることを確認します。そ
の後、3次の精度はないことを示します。
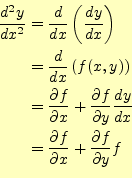
![[*]](crossref.png) )の右辺のテイラー展開の2次の項は、以下の通りです。
)の右辺のテイラー展開の2次の項は、以下の通りです。
![[*]](crossref.png) )とホイン法の3次の項の式(21)は異なってい
ます。したがって、ホイン法は3次の精度がないことが分かります。少なくと
も2次の精度があって、3次の精度がないことが示され、ホイン法は2次の精度
であることが証明されました。
)とホイン法の3次の項の式(21)は異なってい
ます。したがって、ホイン法は3次の精度がないことが分かります。少なくと
も2次の精度があって、3次の精度がないことが示され、ホイン法は2次の精度
であることが証明されました。
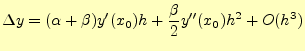
![]() 」
と言ってはいけません。「4次の方が
」
と言ってはいけません。「4次の方が![]() 」と言う輩が出てきます。普通
の科学に携わる人にとって、4次のルンゲ・クッタは常微分方程式の最初で最
後の解法なのです。
」と言う輩が出てきます。普通
の科学に携わる人にとって、4次のルンゲ・クッタは常微分方程式の最初で最
後の解法なのです。