論理回路を用いた1桁の加算器には、下からの桁上げを考慮しない半加算器
(Half Adder)とそれを考慮した全加算器(Full Adder)にが有ります。それぞれ
について、学習します。
入力AとBを加算する回路を考えよう。もちろん、それぞれの入力は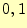 の
いずれかです。1桁の2進数の加算回路です。入出力をブラックボックスで書く
と、図1のようになります。入力
の
いずれかです。1桁の2進数の加算回路です。入出力をブラックボックスで書く
と、図1のようになります。入力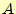 と
と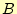 に対して、出
力が
に対して、出
力が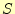 と
と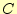 です。
です。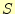 は和を表し英語のSummationから、
は和を表し英語のSummationから、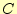 は桁上がりを表
しCarry の頭文字です。このように、入出力だけ示して、中身が分からないも
のブラックボックスと言います。この1ビットの加算のブラックボックスの機
能は、
は桁上がりを表
しCarry の頭文字です。このように、入出力だけ示して、中身が分からないも
のブラックボックスと言います。この1ビットの加算のブラックボックスの機
能は、
- 加算する各1ビットを入力
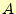 と
と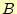 に入れる。実際の回路では、
に入れる。実際の回路では、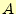 と
と
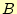 に対応する端子に5Vを印加3する。
に対応する端子に5Vを印加3する。
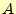 と
と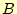 の加算結果の1桁目を
の加算結果の1桁目を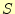 から、桁上がりを示す2桁目を
から、桁上がりを示す2桁目を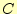 か
ら出力する。実際の回路では、
か
ら出力する。実際の回路では、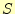 と
と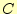 に対応する端子に5Vが出力され
る。
に対応する端子に5Vが出力され
る。
です。これが、2進数の1桁の加算に必要な入出力の全てです。
さて、中身の回路はどうなっているのでしょうか?。それを考えるには、真理
値表を書いてみるのが最も良いでしょう。入出力から、真理値表は表
2のようになります。
表 1:
半加算器の真理値表
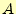 |
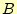 |
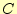 |
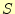 |
| 0 |
0 |
0 |
0 |
| 0 |
1 |
0 |
1 |
| 1 |
0 |
0 |
1 |
| 1 |
1 |
1 |
0 |
残る問題は、この真理値表を実現する回路を設計することだけです。真理値表
から、論理回路を求める方法はいろいろ有りますが、この程度で有れば主加法
標準形に直すのが簡単でしょう。それぞれは、
となります。式(1)の方は排他的論理和(Exclusive OR)と呼ばれ
と書かれることも多いです。排他的論理和については、付録を参照のこと。論
理式ができたので、それを回路に直すだけです。これらを表す論理回路は、図
2や3になります。1桁の半加算器
はこれでおしまい。
図 2:
ORとAND、NOTによる半加算器。式(1)と
(2)の回路
|
|
|
図 3:
XORとANDによる半加算器。式(3)と
(2)の回路
|
|
|
先ほどの半加算器は、入力が演算の対象の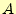 と
と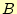 だけでしたで、1桁の2ビッ
トの加算しかできません。実際、複数の桁の加算を行う場合、下位からの桁上
がりも考慮する必要があります。この下位からの桁上がりを考慮した回路が全
加算器です。全加算器の入出力をブラックボックスで書くと、図
4のようになります。入力は3個の1桁の2進数なので、ブ
ラックボックスの入力端子は3個になります。一方、出力はその和をあらわし、
その最大は2桁の
だけでしたで、1桁の2ビッ
トの加算しかできません。実際、複数の桁の加算を行う場合、下位からの桁上
がりも考慮する必要があります。この下位からの桁上がりを考慮した回路が全
加算器です。全加算器の入出力をブラックボックスで書くと、図
4のようになります。入力は3個の1桁の2進数なので、ブ
ラックボックスの入力端子は3個になります。一方、出力はその和をあらわし、
その最大は2桁の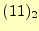 となります。従って、出力端子は2個必要になります。
となります。従って、出力端子は2個必要になります。
先ほどと同じように、真理値表からこのブラックボックス内部の論理回路を考
えます。演算の対象が2つから3つに変わっただけです。3つの1ビットの和を考
えればよいのです。その加算の演算の真理値表を表![[*]](crossref.png) に示します。
に示します。
表 2:
全加算器の真理値表
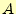 |
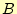 |
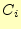 |
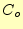 |
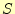 |
| 0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
1 |
| 0 |
1 |
0 |
0 |
1 |
| 0 |
1 |
1 |
1 |
0 |
| 1 |
0 |
0 |
0 |
1 |
| 1 |
0 |
1 |
1 |
0 |
| 1 |
1 |
0 |
1 |
0 |
| 1 |
1 |
1 |
1 |
1 |
真理値表ができたので、次はこれから論理式を作ります。標準展開を用いて論
理式を書くこともできますが、ここではカルノー図を使うのが適当でしょう。
この真理値表の出力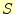 と
と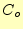 それぞれのカルノー図は、図
それぞれのカルノー図は、図![[*]](crossref.png) と6のようになります。
これから、論理式を導き出しましょう。論理式は、いろいろな形に展開可能で
すが、半加算器の結果の式(1)や(2)、
(3)に近い形に変形することを考えます。これは後で分かる
ように、全加算器は半加算器とORゲートで可能であることを示すためです。
と6のようになります。
これから、論理式を導き出しましょう。論理式は、いろいろな形に展開可能で
すが、半加算器の結果の式(1)や(2)、
(3)に近い形に変形することを考えます。これは後で分かる
ように、全加算器は半加算器とORゲートで可能であることを示すためです。
図 5:
全加算器の和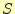 のカルノー図。 のカルノー図。
|
|
|
図 6:
全加算器の桁上がり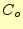 のカルノー図。 のカルノー図。
|
|
|
最初に述べたように、全加算器は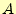 と
と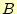 、
、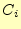 の和と桁上がりを計算して
いる回路です。従って、
の和と桁上がりを計算して
いる回路です。従って、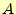 と
と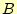 、
、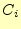 には区別は全くありません。従って、
出来上がった論理式は、それらを入れ替えても成り立つ必要があります。この
ようなことを考えながら、式の展開を行うと計算が上手になります。
には区別は全くありません。従って、
出来上がった論理式は、それらを入れ替えても成り立つ必要があります。この
ようなことを考えながら、式の展開を行うと計算が上手になります。
まず初めに和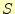 の論理式を求めますが、そのとき以下の排他的論理和の否定
の式を使います。
の論理式を求めますが、そのとき以下の排他的論理和の否定
の式を使います。
これに注意しながら、カルノー図から求められた主加算標準形の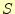 を以下の
ように変形します。
を以下の
ように変形します。
非常にきれいな式が出来上がりました。
つぎに、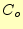 の論理式を作ります。これもカルノー図から、
の論理式を作ります。これもカルノー図から、
となります。
以上で全加算器の論理式が完成したわけですが、もうひとひねりしておきます。
それは、半加算器の式(2)と(3)を用いて、全加
算器の式(5)と(6)を書き直します。ちょっと記号
の問題がありますので、半加算器の出力を
と置き換えます。すると、
となります。ここで、最後のひねりとして、
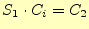 を加えます。
すると
を加えます。
すると
となります。これで準備は完了です。
これらの式をゲートで組み立てる前に、最後の式(11)
と(12)から、全加算器は半加算器2個とORゲートでで
きることが分かります。即ち、図7の
通りです。この半加算器とORゲートを使った動作は、全加算器として動作する
ことが直ぐに理解できると思います。
図 7:
2個の半加算器とORゲートで構成される全加算器
|
|
全加算器が半加算器とORゲートで出来ることが分かったので、論理回路も同じ
ことです。やはり半加算器2個と1個のORゲートで出来ます。図
8と9の通りです。それぞれ
の論理回路がどの式と対応しているかは分かりますよね。考えてください。全
加算器はこれで終わり。
図 8:
ORとAND、NOTゲートによる全加算器
|
|
図 9:
XORとAND、ORゲートによる全加算器
|
|
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年8月20日
![[*]](crossref.png) に示します。
に示します。
![]() と
と![]() それぞれのカルノー図は、図
それぞれのカルノー図は、図![[*]](crossref.png) と6のようになります。
これから、論理式を導き出しましょう。論理式は、いろいろな形に展開可能で
すが、半加算器の結果の式(1)や(2)、
(3)に近い形に変形することを考えます。これは後で分かる
ように、全加算器は半加算器とORゲートで可能であることを示すためです。
と6のようになります。
これから、論理式を導き出しましょう。論理式は、いろいろな形に展開可能で
すが、半加算器の結果の式(1)や(2)、
(3)に近い形に変形することを考えます。これは後で分かる
ように、全加算器は半加算器とORゲートで可能であることを示すためです。
![]() と
と![]() 、
、![]() の和と桁上がりを計算して
いる回路です。従って、
の和と桁上がりを計算して
いる回路です。従って、![]() と
と![]() 、
、![]() には区別は全くありません。従って、
出来上がった論理式は、それらを入れ替えても成り立つ必要があります。この
ようなことを考えながら、式の展開を行うと計算が上手になります。
には区別は全くありません。従って、
出来上がった論理式は、それらを入れ替えても成り立つ必要があります。この
ようなことを考えながら、式の展開を行うと計算が上手になります。
![]() の論理式を求めますが、そのとき以下の排他的論理和の否定
の式を使います。
の論理式を求めますが、そのとき以下の排他的論理和の否定
の式を使います。
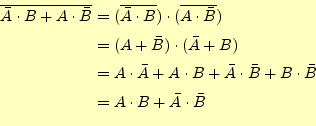
![]() の論理式を作ります。これもカルノー図から、
の論理式を作ります。これもカルノー図から、