2 真理値表からMIL記号への変換

論理変数の少ない真理値表から、簡単な回路を作るためには

1. 真理値表をカルノー図に変換する。
2. カルノー図から論理式に変換する。
3. 論理式を論理回路に変換する。

の手順で作業を進めるのが良いであろう。

2.1 表11の答

問題の表11を1に着目したカルノー図に変換すると、図1のよう になる。これから、論理式は

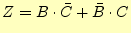$$Z=B\cdot \bar{C}+\bar{B}\cdot C$$ (1)

となる。この論理式から、論理回路は図2と書き表せる。

図 1: 問題の表11のカルノー図

図 2: 問題の表11の論理回路

2.2 表12の答

問題の表12を1に着目したカルノー図に変換すると、図3のよう になる。これから、論理式は

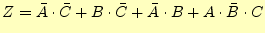$$Z=\bar{A}\cdot\bar{C}+B\cdot\bar{C}+\bar{A}\cdot B +A\cdot\bar{B}\cdot C$$ (2)

となる。この論理式から、論理回路は図4となる。

図 3: 問題の表12のカルノー図

図 4: 問題の表12の論理回路

ここで、少し疑問が涌く。先ほどの1に着目したカルノー図では、論理式の項 数は4であるが、0に着目するとそれは3になる(図5)。0に着目 した場合の方が、簡単になる可能性があるので実際に論理回路を書いてみる。 まず、論理式は

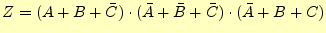$$Z=(A+B+\bar{C})\cdot(\bar{A}+\bar{B}+\bar{C})\cdot(\bar{A}+B+C)$$ (3)

となる。この論理式から、論理回路は図6となる。こちらのほ うが少し簡単と思われる。しかし、正確なことを言うためには、簡単の定義を する必要がある。論理回路が簡単の定義は難しいので、この講義ではそのこと について述べない。試験では、1または0に着目した場合のカルノー図を作成し て、それから求められた論理回路を書けば正解とする。

図 5: 問題の表12のカルノー図(0に着目)

図 6: 問題の表12の論理回路

2.3 表13の答

問題の表13を1に着目したカルノー図に変換すると、図7のよう になる。これから、論理式は

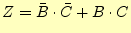$$Z=\bar{B}\cdot \bar{C}+B\cdot C$$ (4)

となる。この論理式から、論理回路は図8となる。

図 7: 問題の表13のカルノー図

図 8: 問題の表13の論理回路

このカルノー図は、左右対称なので0に着目したカルノー図でも、簡単化の度 合いは同じようなものである。

ホームページ: Yamamoto's laboratory
著者: 山本昌志